Engineering topological chiral transport in a flat-band lattice of ultracold atoms

Abstract

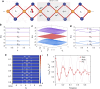
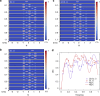
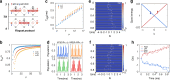
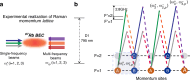
The manipulation of particle transport in synthetic quantum matter is an active research frontier for its theoretical importance and potential applications. Here we experimentally demonstrate an engineered topological transport in a synthetic flat-band lattice of ultracold ⁸⁷Rb atoms. We implement a quasi-one-dimensional rhombic chain with staggered flux in the momentum space of the atomic condensate and observe biased local oscillations that originate from the flat-band localization under the staggered synthetic flux. Based on these features, we design and experimentally confirm a state-dependent chiral transport under the periodic modulation of the synthetic flux. We show that the phenomenon is associated with the topology of the Floquet Bloch bands of a coarse-grained effective Hamiltonian. Our work opens the new avenue for exploring flat-band-assistant topological transport with ultracold atoms, and offers a new strategy for designing efficient quantum device with topological robustness.

Fig. 1. Schematic of the rhombic flux-staggered chain and the breathing mode.

a Schematics of a rhombic flux-staggered chain with flexibly programmable artificial gauge fields. The subfigure shows the binary flux-staggered ladder configuration with a static synthetic flux setting. The complex hopping coefficients between the nearest-neighbor sites are denoted as $J{e}^{i{\theta }_m}(m=1,2,3,4)$. b–d The energy dispersion E(k) of the binary-flux lattice chain with ϕ₂ = π. All the bands display complete flat-band features no matter what ϕ₁ is. b When ϕ₁ ≠ ± π, the binary-flux lattice has six flat bands, labeled as E_±2, E_±1, E₀ respectively. The central band with E₀ is two-fold degenerate. Here we choose ϕ₁ = 0, under which the splitting of the upper and lower bands is the largest. d The flat-band splitting with the variation of ϕ₁. e The evolution dynamics for an initial state $\mid {\psi }_{ini}⟩=\frac{1}{\sqrt{2}}({\widehat{a}}_n^{†}+{\widehat{a}}_{n+1}^{†})\mid 0⟩$ with the binary-flux parameter {ϕ₁ = 0, ϕ₂ = π}. The color map represents the measured atom density ρ/ρ_t, normalized by the total density ρ_t at each discrete time slice. f Measuring a damped oscillation of the total population of sites A₀ and A₁ around 0.9 ms. The red solid lines represent the fitting of experimental data, and the pale red line is the numerical results calculated using H_eff in Eq. (1)

Fig. 2. Biased oscillations in the binary flux-staggered lattice.

a The evolution dynamics under {ϕ₁ = 0, ϕ₂ = π}, with the initial state $\mid {\psi }_{ini}⟩={\widehat{a}}_0^{†}\mid 0⟩$. b The evolution dynamics under {ϕ₁ = 0, ϕ₂ = π} with $\mid {\psi }_{ini}⟩={\widehat{a}}_1^{†}\mid 0⟩$. c The evolution dynamics under {ϕ₁ = 2π/3, ϕ₂ = π} with $\mid {\psi }_{ini}⟩={\widehat{a}}_0^{†}\mid 0⟩$. d The extracted $\mathcal{D}\left(t\right)$ with $\mid {\psi }_{ini}⟩={\widehat{a}}_0^{†}\mid 0⟩$ in different BFL parameters setting. The dots are experimental data, and solid lines are numerical simulations using H_eff

Fig. 3. Floquet channel and topological chiral transport.

a The Floquet protocol by exchanging the adjacent synthetic flux at the spectroscopic moments. In the first half T/2 period, the system can be described by the Hamiltonian H₁; In the second half T/2 period, the system is switched to the Hamiltonian H₂. b The theoretical results of optimal flux setting with perfect population transfer. c The calculated optimal half Floquet period time T_opt with perfect transfer corresponding to each ϕ_opt. d The transfer dynamics within the spinor pair with different ϕ₁ settings. The subfigure (d1) shows the population transfer under the {ϕ₁ = 0.2π, ϕ₂ = π} BFL configuration. The last three subfigures (d2–d4) are corresponding to different optimal ϕ₁ = ϕ_opt settings with μ=1, ν = 2, 3, 4, respectively (ϕ_opt,11 is an imaginary number and thus is irrelevant). e, f The experimental results of the Floquet channel with right and left chiral transport, respectively. For the reason that we mainly observe the chiral current represented by the spinor pair sites A_n, it is unnecessary to distinguish the micromotions of atomic density in the B_n and C_n sites. So, we have combined the display of B_n and C_n sites by indicating their total density information. g The quasi-energy spectrum of the Floquet channel protocol with Ω = 2π/T. h The extracted $\mathcal{D}\left(t\right)$ curve of experimental result for the chiral transports of the Floquet channels. To indicate the chiral feature, we add ± signs in the front of D(t) to differentiate the leftward and rightward motions. The solid lines show the numerical simulations. The error bars present the standard deviation of measurements

Fig. 4. Illustration of experimental configuration and momentum-lattice encoding scheme.

a The momentum lattice is constructed with three Raman-Bragg laser pairs, which are indicated with different colors and labeled by their corresponding frequencies $\{{\omega }_j^{+},{\omega }_{j,p}^{-}\}$ (j = 1, 2, 3). b Configuration for the multi-frequency Raman-Bragg couplings. The solid (dashed) lines represent the single-frequency (multi-frequency) lasers. The sites A_n and B_n (C_n) are encoded with the momentum states of hyperfine level F = 1 (F = 2). As shown in the figure, the pairs of momentum states $\{\mid n,a⟩,\mid n,b⟩\}$ and $\{\mid n,b⟩,\mid n+1,a⟩\}$ are all coupled with laser pairs $\{{\omega }_1^{+},{\omega }_{1,p}^{-}\}$, while the corresponding momentum states $\{\mid n,a⟩,\mid n,c⟩\}$, and $\{\mid n,c⟩,\mid n+1,a⟩\}$ are coupled with laser pairs $\{{\omega }_2^{+},{\omega }_{2,p}^{-}\}$ and $\{{\omega }_3^{+},{\omega }_{3,p}^{-}\}$, respectively. The frequencies ${\omega }_{j,p}^{-}$ are tuned to satisfy the two-photon resonant condition. The single-photon detuning is around 2.8 GHz. The hyperfine split between levels F = 1 and F = 2 of ⁸⁷Rb is about 6.8 GHz