This is a preprint.
Phase separation and coexistence in spatial coordination games between microbes
- PMID: 40964335
- PMCID: PMC12439992
- DOI: 10.1101/2025.09.09.675176
Phase separation and coexistence in spatial coordination games between microbes
Abstract
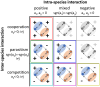
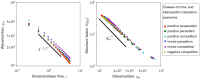
Dense, microbial communities are shaped by local interactions between cells. Both the nature of interactions, spanning antagonistic to cooperative, and the strength of interactions vary between and across microbial species and strains. These local interactions can influence the emergence and maintenance of microbial diversity. However, it remains challenging to link features of local interactions with spatially mediated coexistence dynamics given the significant variation in the microscopic mechanisms involved in cell-to-cell feedback. Here, we explore how microbial interactions over a broad range of ecological contexts spanning antagonism to cooperation can enable coexistence as spatially explicit domains emerge. To do so, we introduce and analyze a family of stochastic coordination games, where individuals do better when playing (i.e., interacting) with individuals of the same type than when playing with individuals of a different type. Using this game-theoretic framework, we show that the population dynamics for coordination games is governed by a double-well shaped interaction potential. We find that in a spatial setting this double-well potential induces phase separation, facilitating coexistence. Moreover, we show that for microbes engaged in symmetric coordination games, phase separation takes on a universal scaling that follows 'Model A' coarsening, consistent with prior experimental observations for Vibrio cholerae mutual killers. Finally, we derive a PDE equivalent of the spatial stochastic game, confirming both the double-well nature of spatial coordination games and the universality of phase separation. Altogether, this work extends prior findings on the link between microbial interactions and population structure and suggests generic mechanisms embedded in local interactions that can enable coexistence.
Figures
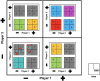

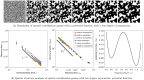
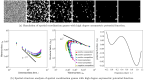
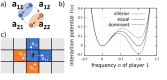

References
-
- Foster K. R. and Bell T., Competition, not cooperation, dominates interactions among culturable microbial species, Current Biology 22, 1845 (2012). - PubMed
-
- Coyte K. Z., Schluter J., and Foster K. R., The ecology of the microbiome: networks, competition, and stability, Science 350, 663 (2015). - PubMed
-
- Nadell C. D., Drescher K., and Foster K. R., Spatial structure, cooperation and competition in biofilms, Nat. Rev. Microbiol. 14, 589 (2016). - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
