Mechanistic within-host mathematical model of inhalational anthrax

Abstract

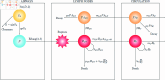
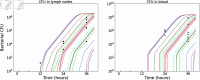
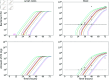
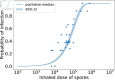
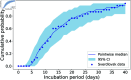
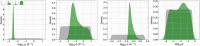
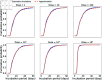
We present a mathematical model of the dynamics of Bacillus anthracis bacteria within the lymph nodes and blood of a host, following inhalation of an initial dose of spores. We also incorporate the dynamics of protective antigen, which is the binding component of the anthrax toxin produced by the bacteria. The model offers a mechanistic description of the early infection dynamics of inhalational anthrax, while its stochastic nature allows us to study the probabilities of different outcomes (for example, how likely it is that the infection will be cleared for a given inhaled dose of spores) in order to explain dose-response data for inhalational anthrax. The model is calibrated via a Bayesian approach, using in vivo data from New Zealand white rabbit and guinea pig infection studies, enabling within-host parameters to be estimated. We also leverage incubation-period data from the Sverdlovsk 1979 anthrax outbreak to show that the model can accurately describe human time-to-symptoms data under reasonable parameter regimes. Finally, we derive a simple approximate formula for the probability of symptom onset before time t, assuming that the number of inhaled spores has a Poisson distribution.

Fig 1. Diagram of the within-host model of inhalational anthrax.

See the Methods section for a detailed description of the model.

Fig 2. Stochastic model realisations compared to the CFU data used in the ABC-SMC for the rabbit model calibration.

A sample of 20 model realisations using the “best” posterior parameter set (the one corresponding to the smallest distance from the data in the ABC-SMC) is compared with the CFU loads in the TBLN (left) and blood (right) of individual rabbits, provided in Table 4.

Fig 3. Posterior predictions of the dose-response curve, compared with the dose-response data used in the ABC-SMC for the rabbit model calibration.

Each parameter set in the posterior sample was used to obtain a prediction from the mechanistic exponential dose-response model given by Eqs (5) and (6). The blue solid line shows the pointwise median of these predictions and the shaded region shows the 95% credible interval. The dots represent the rabbit dose-response data set from Gutting et al. [21], which was used in the calibration.

Fig 4. Posterior distributions for each species.

Kernel density estimates for the prior distribution (grey) and the marginal posterior distribution of each parameter in the rabbit model (blue) and the guinea-pig model (orange). Parameter values that were fixed for the rabbit or guinea-pig model calibration are indicated by vertical blue or orange lines, respectively. For each species, the corresponding posterior distribution was obtained by fitting the mechanistic dose-response curve given by Eqs (5) and (6) to the dose-response data for that species from Gutting et al. [21], and simultaneously fitting the Markov-chain model in Fig 1 to the CFU loads in the TBLN and blood from the rabbit data in Table 4, or the CFU loads and PA amounts in the blood from the guinea-pig data in Table 5.

Fig 5. Stochastic model realisations compared with the CFU and PA data used in the ABC-SMC for the guinea-pig model calibration.

A sample of 10 model realisations using the “best” posterior parameter set (the one corresponding to the smallest distance from the data in the ABC-SMC) is compared with the CFU loads (top row) and PA amounts (bottom row) in the blood of individual guinea-pigs, provided in Table 5.

Fig 6. Posterior predictions of the dose-response curve, compared with the dose-response data used in the ABC-SMC for the guinea-pig model calibration.

Each parameter set in the posterior sample was used to obtain a prediction from the mechanistic exponential dose-response model given by Eqs (5) and (6). The blue solid line shows the pointwise median of these predictions and the shaded region shows the 95% credible interval. The dots represent the guinea-pig dose-response data set from Gutting et al. [21], which was used in the calibration.

Fig 7. Diagram of the simplified within-host model of inhalational anthrax for humans.

See the Methods section for a description of how the model is used to simulate individual incubation periods.

Fig 8. Human incubation period data set from the Sverdlovsk outbreak [19].

Left: Histogram of the number of days to symptom onset for the 30 individuals. Right: Cumulative distribution of number of days to symptom onset.

Fig 9. Pointwise median and 95% credible interval of the model fits to the human incubation period data [19].

For each parameter set in the posterior sample (see Fig 10), a sample of 30 finite incubation periods was obtained from stochastic model simulations. We plot here the median and 95% CI (across all posterior parameter sets) of the cumulative daily fractions of these simulated incubation periods.

Fig 10. Posterior distribution for the human model.

Kernel density estimates for the prior distribution (grey) and the marginal posterior distribution (green) of each parameter in the human model. This posterior distribution was obtained by fitting the simple model in Fig 7 to the Sverdlovsk outbreak incubation periods data set in Fig 8.

Fig 11. Kernel density estimates for the marginal posterior distributions of λ, μ, and ϕ.

These are obtained by transformations of the posterior distribution for σ and p, using Eqs (1) and (2).

Fig 12. Scatter plots showing the relationships between pairs of parameters in the posterior sample for the human model.

Fig 13. Comparison between the incubation period distributions obtained by stochastic model simulations and the approximation in Eq (3).

The doses considered are $1,10,100,{10}^3,{10}^4,$ and 10⁵ inhaled spores. For each dose, the blue line was obtained by simulating 4 × 10² finite incubation periods using the stochastic model. The orange dashed line was obtained by the approximation in Eq (3). The parameter values used were the medians of the marginal posterior distributions in Fig 10: $\rho =0.004{\text{h}}^{-1}$, $\delta =0.107{\text{h}}^{-1}$, $\sigma =0.217{\text{h}}^{-1}$, p = 0.01.