A workflow to discover partial differential equations from data: Application to the dynamics of tree biomass

Abstract

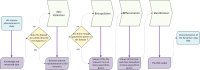
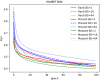
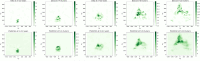
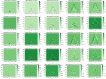
Mixed data and theory driven methods are promising approaches that can be used to bring better understanding of complex dynamics in life sciences. For vegetation growth, integrated knowledge may be lacking to design theoretical models like partial differential equations (PDE). This lack can be complemented by using data. The method presented in this paper is a generic computational workflow called CEDI that aims at discovering PDE models from data. As an illustration, we tested the workflow on biomass dynamics of three different 3D trees of specific architectural types. ● The name CEDI represents the four steps composing the workflow: data Collection, Extrapolation, Differentiation and Identification. ● The originality of this workflow is twofold: first, it encompasses the whole modeling process from the definition of the variables to the design of a PDE, and second it has been designed to be generic in a sense that it can apply to any dynamics and it covers most existing data driven PDE discovering methods. ● The workflow offers a framework to better understand data driven PDE discovering methods and a tool for modeling any dynamics, provided that right data and knowledge and also good algorithm settings are available.

Keywords: Data-driven modelling of plants; Parameter estimation; Physics informed neural network; Theory-guided data model.

Graphical abstract

Fig. 1

The CEDI workflow for PDE discovery from data.

Fig. 2

Tree growth of Massart type. Mock-ups obtained by the AmapSim software.

Fig. 3

Tree growth of Prevost type. Mock-ups obtained with the AmapSim software.

Fig. 4

Tree growth of Rauh type. Mock-ups simulated by the AmapSim software.

Fig. 5

Data flowchart summarizing the CEDI workflow applied to tree biomass dynamics.

Fig. 6

Convergence history of the extrapolation step for the data of Massart, Rauh and Prevost trees and batch size (BS) 2, 16 and 64.

Fig. 7

Biomass of the Massart tree plotted on the $\left(\mathrm{O},{\overrightarrow{\mathrm{e}}}_2,{\overrightarrow{\mathrm{e}}}_3\right)$-plane: data (top) and predicted values (bottom) by the extrapolation with the surrogate model (trained with a batch size of 2).

Fig. 8

Biomass of the Prevost tree plotted on the $\left(O,{\overrightarrow{e}}_2,{\overrightarrow{e}}_3\right)$-plane: data (top) and predicted values (bottom) by the extrapolation with the surrogate model (trained with a batch size of 2).

Fig. 9

Biomass of the Rauh tree plotted on the $\left(\mathrm{O},{\overrightarrow{\mathrm{e}}}_2,{\overrightarrow{\mathrm{e}}}_3\right)$-plane: data (top) and predicted values (bottom) by the extrapolation with the surrogate model (trained with a batch size of 2).

Fig. 10

Massart tree. Plots on the $\left(\mathrm{O},{\overrightarrow{\mathrm{e}}}_2,{\overrightarrow{\mathrm{e}}}_3\right)$-plane of isovalues of the biomass partial derivatives associated with catalogue Ⅱ. The first line shows isovalues of $\frac{\partial \mathrm{B}}{\partial \mathrm{t}}$ at t=2, 4, 6, 8 and 10 years (from left to right). The following lines show isovalues of $\frac{\partial \mathrm{B}}{\partial {\mathrm{x}}_1}$, $\frac{\partial \mathrm{B}}{\partial {\mathrm{x}}_2}$, $\frac{\partial \mathrm{B}}{\partial {\mathrm{x}}_3}$ and $\frac{{\partial }^2\mathrm{B}}{\partial {\mathrm{x}}_1^2}+\frac{{\partial }^2\mathrm{B}}{\partial {\mathrm{x}}_2^2}+\frac{{\partial }^2\mathrm{B}}{\partial {\mathrm{x}}_3^2}$ respectively at t=2, 4, 6, 8 and 10 years (from left to right).

Fig. 11

Convergence histories of the identification step with catalogues Ⅰ to Ⅳ for Massart, Prevost and Rauh trees with batch sizes (BS) 2, 16 and 64.