Hyper Diversity, Species Richness, and Community Structure in ESS and Non-ESS Communities

Abstract

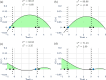
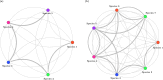
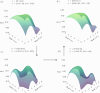
In mathematical models of eco-evolutionary dynamics with a quantitative trait, two species with different strategies can coexist only if they are separated by a valley or peak of the adaptive landscape. A community is ecologically and evolutionarily stable if each species' trait sits on global, equal fitness peaks, forming a saturated ESS community. However, the adaptive landscape may allow communities with fewer (undersaturated) or more (hypersaturated) species than the ESS. Non-ESS communities at ecological equilibrium exhibit invasion windows of strategies that can successfully invade. Hypersaturated communities can arise through mutual invasibility where each non-ESS species' strategy lies in another's invasion window. Hypersaturation in ESS communities with more than 1 species remains poorly understood. We use the G-function approach to model niche coevolution and Darwinian dynamics in a Lotka-Volterra competition model. We confirm that up to 2 species can coexist in a hypersaturated community with a single-species ESS if the strategy is scalar-valued, or 3 species if the strategy is bivariate. We conjecture that at most $n·\left(s+1\right)$ species can form a hypersaturated community, where $n$ is the number of ESS species at the strategy's dimension $s$ . For a scalar-valued 2-species ESS, 4 species coexist by "straddling" the would-be ESS traits. When our model has a 5-species ESS, we can get 7 or 8, but not 9 or 10, species coexisting in the hypersaturated community. In a bivariate model with a single-species ESS, an infinite number of 3-species hypersaturated communities can exist. We offer conjectures and discuss their relevance to ecosystems that may be non-ESS due to invasive species, climate change, and human-altered landscapes.

Supplementary information: The online version contains supplementary material available at 10.1007/s13235-025-00646-2.

Keywords: Darwinian Dynamics; Evolutionary game theory; Hypersaturated communities; Mutual invasibility; Niche coevolution; Non-ESS communities.

Fig. 1

Results for the single strategy (${\mathrm{\sigma }}_{\text{K}}^2=4$) (a, b, c) and two strategy (${\mathrm{\sigma }}_{\text{K}}^2=12.5$) (d, e, f) ESS cases. Colored circles represent species’ strategies. Solid and dotted lines represent the value of the G-function vs strategy value when the resident has the strategy marked by the respective colored circle on the lines. The G-function lines of all the species overlap in c, d, e, and f, and only one line is visible. The dashed vertical lines show the location of the ESS strategy values on the x axis. (a) Single strategy ESS. (b) Invasion windows (light green shaded regions) of each of the two non-ESS species with strategies above and below the ESS when they are the sole population and are at ecological equlibrium. The overlap of the respective invasion windows is the bright green region. (c) Adaptive landscape when the two non-ESS species coexist. (d) Convergent stable minimum before reaching two strategy ESS. (e) Two strategy ESS. (f) Adaptive landscape when 4 non-ESS species coexist

Fig. 2

The non-ESS community shown in Fig. 1f has strategies $\mathbf{u}=(-0.60,-0.10,2.90,3.35)$. Here, the invasion windows of each of the 4 non-ESS species in Fig. 1-f are shown as if the starting conditions reflected each of those four species alone. Invasion windows (light green shaded regions) of species 1 (a) and 4 (d) contain all the other species’ strategies. Invasion windows of species 2 (b) and 3 (c) do not contain one of the other three species’ strategies. Species 3 (c) and 4 (d) have discontinuous invasion windows with valleys separating the two regions of the invasion window. Colored circles represent species’ strategies. Solid lines represent the value of the G-function vs strategy value when the resident has the strategy marked by the respective colored circle on the lines. The vertical dashed lines show the location of the ESS strategy values on the x axis

Fig. 3

The non-ESS community shown in Fig. 1f has strategies $\mathbf{u}=(-0.60,-0.10,2.90,3.35)$. Here, the invasion windows are shown for all combinations of two species as the initial conditions (a, b, d, e) and two three species initial conditions (c, f) non-ESS species coexist. Invasion windows when species 1 and 4 coexist (a), 2 and 3 coexist (d) contain all other strategies within them, whereas 2 and 4 (b) and 1 and 3 (e) do not. The two possible 3-species combinations have invasion windows that contain the fourth strategy (c, f). Colored circles represent species’ strategies. The solid line represents the value of the G-function vs strategy value when the coexisting residents have the strategies marked by the colored circle on the lines. The vertical dashed lines show the location of the ESS strategy values on the x axis

Fig. 4

a, d, e, b show stages of evolutionary branching with convergent stable equilibria before reaching the 5 species ESS (c). Adding species on each side of the 5 ESSs leads to 3 species going extinct and 7 species coexisting (f). The insets above (f) show the two species around peak 1 (left inset, blue species does not survive) and peak 5 (right inset, both species survive). Colored circles represent species’ strategies. The solid line represents the value of the G-function vs strategy value when the residents have the strategies marked by the colored circle on the lines. The vertical dashed lines show the location of the ESS strategy values on the x axis. The (bright-) light-green shaded regions represent (overlapping) invasion windows (Color figure online)

Fig. 5

Network depicting the effect of competition of each species on the others for the 5 ESS species (a) and 7 non-ESS species (b) systems. The nodes represent the species and edge thickness denotes the effect of competition of the source species on the sink species. In (a), the effect of competition is greatest from the immediate neighbor with higher strategy value. In hypersaturated communities, the interactions are stronger because more species are very similar (b)

Fig. 6

a The single species ESS when vector-valued traits are considered. b Coexistence of three non-ESS species. c Interaction network of the three non-ESS species. Here ${\mathrm{\sigma }}_{\text{K}}^2=2$. Colored circles represent species’ (vector-valued) strategies. The surface represents the value of the G-function vs strategy values when the residents have the strategies marked by the colored circle on the surfaces. The vertical dashed lines show the location of the ESS strategy values on the trait 1-trait 2 plane. The color gradient on the surface scale the value of the highest fitness (green) relative to the lowest (purple) invasion windows (Color figure online)

Fig. 7

Invasion windows of each of the three non-ESS species (a–c) and when they coexist in pairs (d–f) Each invasion window contains the other species’ strategies (marked by crosses). Colored circles represent species’ (vector-valued) strategies. The surface represents the value of the G-function vs strategy values when the residents have the strategies marked by the colored circle on the surfaces. The vertical dashed lines show the location of the ESS strategy values on the trait 1-trait 2 plane. The color gradient on the surface scale the value of the highest fitness (green) relative to the lowest (purple) invasion windows (Color figure online)

Fig. 8

Fitness landscape at different times (progressing anti-clockwise, a-c-d-e) when a new species is added with ${\mathrm{\sigma }}_{\text{K}}^2=14$. When a second species is introduced at $\mathbf{u}=(0.17,-0.05)$ (orange dot, top of the landscape in (a)) with the resident species at the saddle point (blue dot in (a)), the adaptive landscape changes drastically. Soon, a valley forms (c) and the resident is pushed out and goes extinct, and the new species evolves back towards the saddle point (d, b). Colored circles represent species’ (vector-valued) strategies. The surface represents the value of the G-function vs strategy values when the residents have the strategies marked by the colored circle on the surfaces. The color gradient on the surface scale the value of the highest fitness (green) relative to the lowest (purple) invasion windows (Color figure online)