Hexagonal Zn1-xMgxS sheds light on the lattice dynamics of atomic alloys

Abstract

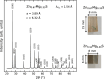
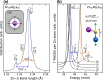
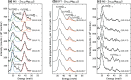
Cubic pseudo-unary A_1-xB_x high-entropy metallic alloys and pseudo-binary A_1-xB_xC disordered semiconductor alloys set a benchmark to explore how physical properties are impacted by disorder. Through its diversity, the lattice dynamics offers a unique playground to assign the relevant length scales at which operate various kinds of disorders induced by alloying. (i) In high-entropy metallic alloys, the overdamping of the bond-collective (multi-bond→1-mode) acoustic modes at short wavelength originates from force-constant fluctuations. (ii) In semiconductor alloys, the lattice mismatch splits, at any wavelength, the bond-specific (1-bond→1-mode) optical modes in duos distinguishing "same" from "alien" environments, as explained by the percolation model. Zn_1-xMg_xS is ideal to test both univocal assignments. Its force-constant disorder is small, reducing the cause for overdamping of the acoustic modes. Its local strain is inverted, the lighter substituent being the larger one and forming the longer bond. This forecasts a dramatic inversion of the mode-duos. Further, its wurtzite structure enables (iii) to test whether/how the percolation model for the mode-duos transfers under lowering the crystal symmetry from cubic to hexagonal. The triple acoustic-(i)/optical-(ii-iii) test on Zn_1-xMg_xS, combining inelastic neutron scattering with first-principles simulations, is positive. This highlights a few key points behind the lattice dynamics of atomic alloys.

Fig. 1

Zn_1 − xMg_xS crystals – size and structure. Powder X-ray diffractogram obtained at ambient conditions with wurtzite-Zn_0.67Mg_0.33S. The individual peaks are labelled via the (hkl) Miller indices. The corresponding lattice parameters (a and c) are indicated. Photographs of the cleaved semi-cylindrical Zn_1 − xMg_xS single crystals studied by INS are shown on the right. The axis of wurtziteZn_0.67Mg_0.33S, co-oriented by conoscopy, X-ray diffraction and neutron diffraction in situ, lies in-plane, i.e., within the cleaved face, tilted by ~ 45° with respect to the ingot axis, as indicated by the arrow.

Fig. 2

Polarized Raman spectra of wurtzite-Zn_0.67Mg_0.33S. Polarized Raman spectra addressing the high-frequency bond-specific non-polar Raman active and -modes of wurtziteZn_0.67Mg_0.33S taken at normal incidence/detection onto/through parallel cleaved crystal faces in backward or forward scattering geometries. and are allowed and is forbidden in the and geometries. and are forbidden and is allowed in the geometry. In forward scattering the polar Zn-S and Mg-S soften on entering the phonon-polariton (PP) regime, revealing the non-polar (not subject to phonon-polariton coupling). In each symmetry, the Raman signal signal is obscured by a sharp antiresonance (marked by a star) due to a Fano interference. The vibration patterns of the high-frequency bond-specific (upper four) and low-frequency bond-collective (lower two) optical modes in the wurtzite structure are sketched out.

Fig. 3

Ab initio insight into the origin of the Zn-S PM-duo of wurtzite-Zn_1 − xMg_xS (~0). (a) Ab initio distribution of Zn-S (subscript) bond lengths () in a large ZnS-like supercell involving a unique ZnMg substitution corresponding to different bond lengths near Mg (hetero environment) and far from it (homo environment, first superscript) either along the axis or perpendicular to it (second superscript). Inset: The long Mg-bonds generate a compressive strain within their first-neighbour Mg-shell, delimited by a dotted curve, as sketched out (omitting the anisotropy of the crystal structure). (b) Corresponding PM-duo of Zn-S optical () mode, labelled using the same subscript/superscript code, generated ab initio by projecting the phonon density of states per Zn atom at the BZ-center (-PhDOS). The ,, and symmetries are separately addressed, as indicated. Inset: The local -like Zn-S stretching in presence of Mg is sketched out to fix ideas (the exact atom displacement looks like that shown in Fig. 4 except that the Mg and Zn roles should be reversed).

Fig. 4

Ab initio insight into the origin of the Mg-S PM-duo of wurtzite-Zn_1 − xMg_xS (~1). (a) Ab initio distribution of Mg-S bond lengths () in a large MgS-like supercell involving a unique ZnMg substitution, corresponding to different bond lengths near Zn (hetero environment) and far from it (homo environment, first superscript) either along the axis or perpendicular to it (second superscript). Inset: The short Zn-bonds generate a tensile strain within their first-neighbour Zn-shell, delimited by a dotted curve, as sketched out (omitting the anisotropy of the crystal structure). (b) Corresponding PM-duo of Mg-S optical () mode, labelled by using the same subscript/superscript code, generated ab initio by projecting the phonon density of states per S atom at the Brillouin zone center (-PhDOS). The ,, and symmetries are separately addressed, as indicated. (c) Snapshot of atom displacements of the -like minor- mode, highly-localized (red arrows) near Zn (colored in blue).

Fig. 5

Wurtzite-Zn_0.67Mg_0.33S phonon dispersion. (a, b) Experimental (INS) and ab initio (DFT) wurtzite-Zn_0.67Mg_0.33S phonon dispersions along and sampled using reciprocal lattice units (r.l.u.). Dotted curves are guide for the eye. The experimental (matching the INS resolution) and ab initio (due to uncertainty on peak positions) error bars are within the symbol size. The shaded rectangles emphasize Zn-S and/or Mg-S PM-duos for the top-listed -modes. In each -duo the lower and upper modes refer to Zn- and Mg-like environments, as indicated (superscript) for the ZnS-like (subscript) mode [panel (b)]. The shaded/hollow circles emphasize the crossing of acoustic and optical modes with same/different polarizations. Halfway the dispersion along , an effective coupling develops between and – not visible, manifested by the anticrossing of the coupled modes, symbolized in order of frequency.

Fig. 6

wurtzite-Zn_1 − xMg_xS phonon dispersion. (a) wurtzite-Zn_0.67Mg_0.33S phonon dispersion measured by INS along . The dual Zn-S and Mg-S signals (-subscript) are deconvolved (colored dashed lines), distinguishing homo from hetero environments (-superscript). is activated specifically at the Brillouin zone center, as indicated. (b) Corresponding dispersion per S atom calculated ab initio (DFT) by using the vertical wurtzite-Zn_0.67Mg_0.33S special quasirandom structure shown in Fig. S2. (c) The same dispersion measured by INS with wurtzite-Zn_0.94Mg_0.06S.

Fig. 7

phonon dispersion of wurtzite-Zn_1 − xMg_xS. (a) phonon dispersion of wurtzite-Zn_0.67Mg_0.33S measured by INS along . The dual Zn-S signal (subscript) is deconvolved for clarity (colored dashed lines), distinguishing homo from hetero environments (superscript). is activated specifically at the Brillouin zone center, as indicated. (b) Corresponding phonon dispersion per S atom calculated ab initio (DFT) by using the horizontal wurtzite-Zn_0.67Mg_0.33S special quasirandom structure shown in Fig. S2. (c) Corresponding phonon dispersion of wurtziteZn_0.94Mg_0.06S measured by INS.

Fig. 8

coupling along in wurtzite-Zn_1 − xMg_xS. (a) Ab initio (DFT) -projected (dotted curves) and (solid curves) PhDOS per cation (summed across Zn and Mg) behind the corresponding () coupled modes, completing the cumulated -projected PhDOS per anion (S) along provided in Fig. S5. (b, c) Corresponding model (plain curves) of two mechanically-coupled harmonic oscillators using 40. (b) Dispersion of coupled modes () measured by INS (solid symbols, Fig. S5a) and predicted ab initio [DFT, hollow symbols, panel (a)]. The ab initio frequencies are marred by error bars estimated from the width at half mawimum of the ab initio lines [an example is given in panel (a) – double arrows]. (c) Relative contributions of (via ) and (via ) to the coupled mode () depending on ; and vice versa for the coupled mode ().

Fig. 9

Low-frequency phonon dispersions of wurtzite-Zn_0.67Mg_0.33S along . (a, b) (blue)+ (orange) and + phonon dispersions of wurtzite-Zn_0.67Mg_0.33S measured by INS along . (c, d) Corresponding ab initio (DFT) data obtained by using the relevant (right) special quasirandom structure shown in Fig. S2.