Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2025 Oct 7;15(1):34949.
doi: 10.1038/s41598-025-18870-6.

Lower bounds for the Zagreb indices of trees with given total domination number and its applications in QSPR studies of alkanes

Merin Manuel  1 , A Parthiban  2
Affiliations

Lower bounds for the Zagreb indices of trees with given total domination number and its applications in QSPR studies of alkanes

Merin Manuel et al. Sci Rep. .

Abstract

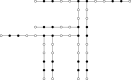
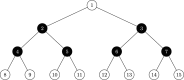
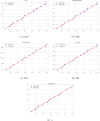
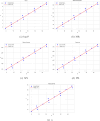
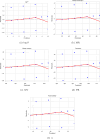
Understanding the relationship between molecular structure and physicochemical properties is a central problem in mathematical chemistry and molecular informatics. Among the many topological descriptors used for this purpose, Zagreb indices play a significant role due to their proven relevance in quantitative structure-property relationship (QSPR) studies. Motivated by the need for structural insight into molecules modeled as trees, this work focuses on deriving lower bounds for the first and second Zagreb indices of trees with a fixed total domination number. By analyzing the structural properties of such trees, we establish new inequalities that highlight the interplay between domination parameters and molecular descriptors. To validate their practical relevance, we apply the derived bounds in a QSPR context, specifically examining their correlation with key physicochemical properties of alkanes. The statistical analysis reveals strong predictive capability, with near-to-unity correlation coefficients between the computed bounds and experimental data. These results demonstrate the potential of domination-theoretic methods in advancing predictive modeling in chemical graph theory.

Keywords: Extremal trees; QSPR analysis; Total domination number; Zagreb indices.

PubMed Disclaimer

Conflict of interest statement

Declarations. Competing interests: The authors declare no competing interests.

Figures

Fig. 1
Fig. 1
A tree from formula image with formula image and formula image.
Fig. 2
Fig. 2
Trees for Claims 1, 2, 3, and 4, respectively.
Fig. 3
Fig. 3
Trees for Claims 5, 6, and 7, respectively.
Fig. 4
Fig. 4
Trees for Claims 8, 9, and 10, respectively.
Fig. 5
Fig. 5
A full binary tree B on 15 vertices.
Fig. 6
Fig. 6
Linear regression fit diagrams for physicochemical properties related to formula image.
Fig. 7
Fig. 7
Linear regression fit diagrams for physicochemical properties related to formula image.
Fig. 8
Fig. 8
Residual plots related to formula image.
Fig. 9
Fig. 9
Residual plots related to formula image.
See this image and copyright information in PMC

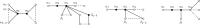
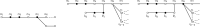
References

    1. Trinajstic, N. Chemical Graph Theory (CRC Press, Boca Raton, 2018).
    1. Gutman, I. & Trinajstić, N. Graph theory and molecular orbitals. Total formula image electron energy of alternant hydrocarbons. Chem. Phys. Lett.17(4), 535–538 (1972).
    1. Cockayne, E. J., Dawes, R. & Hedetniemi, S. T. Total domination in graphs. Networks10(3), 211–219 (1980).
    1. Das, K. C., Huh, D.-Y., Bera, J. & Mondal, S. Study on geometric-arithmetic, arithmetic-geometric and Randić indices of graphs. Discrete Appl. Math.360, 229–245. 10.1016/j.dam.2024.09.007 (2025).
    1. Mondal, S., Das, K. C. & Huh, D. The minimal chemical tree for the difference between geometric-arithmetic and Randić indices. Int. J. Quantum Chem.124(1), 27336. 10.1002/qua.27336 (2024).

LinkOut - more resources