Attention to quantum complexity

Abstract

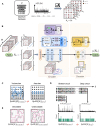
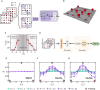
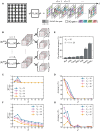
The imminent era of error-corrected quantum computing demands robust methods to characterize quantum state complexity from limited, noisy measurements. We introduce the Quantum Attention Network (QuAN), a classical artificial intelligence (AI) framework leveraging attention mechanisms tailored for learning quantum complexity. Inspired by large language models, QuAN treats measurement snapshots as tokens while respecting permutation invariance. Combined with our parameter-efficient miniset self-attention block, this enables QuAN to access high-order moments of bit-string distributions and preferentially attend to less noisy snapshots. We test QuAN across three quantum simulation settings: driven hard-core Bose-Hubbard model, random quantum circuits, and toric code under coherent and incoherent noise. QuAN directly learns entanglement and state complexity growth from experimental computational basis measurements, including complexity growth in random circuits from noisy data. In regimes inaccessible to existing theory, QuAN unveils the complete phase diagram for noisy toric code data as a function of both noise types, highlighting AI's transformative potential for assisting quantum hardware.

Fig. 1.. Learning relative complexity between states ρα and ρβ from bit-string collections.

(A) Measurements of a quantum state $\mathrm{\rho }$ samples bit-strings $\left\{B_i\right\}$ from bit-string probability distribution $p\left(\right\{b_i\}\mid \mathrm{\rho })$ over the $2^{N_{\mathrm{q}}}$-dimensional Hilbert space. (B) Schematic architecture of the QuAN. The $Z$-basis snapshot collection of size $M$ is partitioned into sets $\left\{{\mathbb{X}}_i\right\}$ of size $N$ . In the encoder stage, after convolution registers positions of qubits, the set goes through $L$ layers of the MSSAB. Inside the MSSAB, the input is further partitioned into $N_{\mathrm{s}}$ minisets to be parallel processed through SABs, recurrent attention block (RecAB), and reducing attention block (RedAB). The decoder stage compresses the output from the encoder, allowing for attending to different components in a permutation-invariant manner, using a PAB and single-layer perception (SLP). The output label is $y=1$ for the state ${\mathrm{\rho }}_{\mathrm{\alpha }}$ and $y=0$ for the state ${\mathrm{\rho }}_{\mathrm{\beta }}$ . See Supplementary Materials section A for more details. (C to E) Examples of ${\mathrm{\rho }}_{\mathrm{\alpha }}$ and ${\mathrm{\rho }}_{\mathrm{\beta }}$ for learning relative complexity using the binary classification output of the QuAN. (C) Volume-law entangled state versus area-law entangled state. The entanglement between two subsystems (white and gray) is indicated through blue links. (D) Random circuit state at depth $d$ versus that at some deep reference depth. (E) Decodable versus undecodable states of an error-correcting code under noise. The incoherent noise depicted in gray suppresses large loops.

Fig. 2.. Relative complexity between volume-law and area-law scaling states.

(A) Intersnapshot correlation reveals $X-X$ correlation of the quantum state. The purple box shows the schematic of the SAB capturing the intersnapshot correlation. (B) Schematic diagram of the 16-transmon-qubit chip used for quantum emulation of the driven hard-core Boson-Hubbard model. (C) Entanglement transition based on the scaling of bipartite entanglement entropy $S=S_{A}A+S_{V}V$ , where $A$ and $V$ represent the area and volume of the subsystem, respectively. Adapted from Karamlou et al. (45) (https://creativecommons.org/licenses/by/4.0/). (D) Schematic of a contrast architecture: The SMLP respects the permutation symmetry. (E to G) Average confidence $\overline{y}$ as a function of detuning strength $\mathrm{\delta }$ for different architectures using different set sizes $N$ . The star symbol marks the training points. The average and errors are obtained from 10 independent model training. For machine learning details, see Supplementary Materials section C2. (E) The SMLP fails to train. (F) QuAN₂ ( $N_{\mathrm{s}}=1$ , $L=1$ ). (G) QuAN₄ with two layers of self-attention ( $N_{\mathrm{s}}=1$ , $L=2$).

Fig. 3.. Relative complexity between the random circuit state at depth d and the reference state at depth d = 20.

(A) Schematic illustration of the 6-by-6 subarray of qubits from Google’s “Sycamore” quantum processor. A random circuit of depth $d$ alternates entangling iSWAP-like gates (gray) and single-qubit (SQ) gates randomly chosen from the set $\left\{\sqrt{X^{\pm 1}},\sqrt{Y^{\pm 1}},\sqrt{W^{\pm 1}},\sqrt{V^{\pm 1}}\right\}$ , with $W=(X+Y)/\sqrt{2}$ and $V=(X-Y)/\sqrt{2}$ . The two-qubit gates are applied in a repeating series of ABCDCDAB patterns. (B) Data structure. For each depth $d$ , we sample $N_{\mathrm{c}}=50$ circuits. For each circuit instance $s$ , we sample $M_s$ bit-strings and partition them into sets of size $N$ , resulting in a total of $N_{\mathrm{c}}\times M_s/N$ sets for each circuit depth $d$ . (C) XEB (Eq. 5) for bit-strings from noiseless simulations as a function of circuit depth $d$ with varying system sizes $N_{\mathrm{q}}$ . The markers show the averaged XEB over $N_{\mathrm{c}}=50$ different circuit instances and the error bars for the standard errors. (D) Pure-state trained QuAN₅₀’s classification accuracy for pure-state data. We train eight independent models at each circuit depth $d$ and show the averaged accuracy (marker) and the standard error (error bar). QuAN₅₀ successfully learns the relative complexity of $d=8$ . (E) Comparison of the performances of QuAN₂, QuAN₅₀, and other architectures in learning the relative complexity of depth $d=8$ on an $N_{\mathrm{q}}=25$ qubit system. The models maintain approximately the same total number of trainable parameters to make a controlled comparison between different architectures. (F) Averaged XEB for experimentally collected bit-strings. The plot shows the averaged XEB over 50 circuit instances (markers) and the standard error (error bars). The XEB smoothly decays as a function of depth $d$ . (G) Learning relative complexity from experimental data using QuAN₅₀ trained on noiseless data.

Fig. 4.. Learning the relative complexity of decodable and undecodable states of the toric code.

(A) Transformation from the $Z$-basis measurements to the smallest-loop, plaquette variables. (B) The QuAN can build larger closed loops through multiplication. (C and D) Decodability phase diagram of the toric code state under coherent and incoherent noise for two different set sizes: $N=1$ in (C) and $N=64$ in (D). The regions in the phase space that support the training data are marked with hatch marks. The average confidence $\overline{y}$ averages over 10 independent model training. The known thresholds are marked along the $g_X=0$ axis at $p_{\mathrm{c}}\approx 0.11$ and along the $p_{\text{flip}}=0$ at $g_{\mathrm{c}}\approx 0.22$ . (E) Average confidence $\overline{y}$ by QuAN₂ for different set sizes $N$ and by the SMLP with $N=64$ along the axis $g_X=0$ . The error bar shows the standard error for $\overline{y}$ over 10 independent model training. (F) Average confidence $\overline{y}$ by QuAN₂ with varying set sizes $N$ and by the SMLP with $N=64$ along the axis $p_{\text{flip}}=0$ . (G) Average confidence $\overline{y}$ by QuAN₂ and the PAB with $N=64$ along the axis $g_X=0$ , where the PAB is defined as the model without self-attention and has only pooling attention. (H) Average confidence $\overline{y}$ by QuAN₂ and the PAB with $N=64$ along the axis $p_{\text{flip}}=0$ . (I) Pooling attention score histogram from the topological state with $(g_X,p_{\text{flip}})=\left(\mathrm{0,0.05}\right)$ . (J) Loop expectation value $\langle Z_{\text{closed}}\rangle$ as a function of the loop perimeter for high- and low-attention-score snapshots in the topological state with $(g_X,p_{\text{flip}})=\left(\mathrm{0,0.05}\right)$ . The error bars represent the standard error of $\langle Z_{\text{closed}}\rangle$ over different loop configurations in corresponding snapshots.