Allocentric flocking

Abstract

Understanding how group-level dynamics arise from individual interactions remains a core challenge in collective behavior research. Traditional models assume animals follow simple behavioral rules, like explicitly aligning with neighbors. We present here an alternative theoretical framework that considers collective behavior to be grounded in neurobiological principles-particularly that animals employ ring attractor networks to encode bearings towards objects in space in an allocentric (i.e., with respect to a fixed external reference frame, such as a stable landmark) and/or egocentric (i.e., the angle relative to the animal's heading) neural coding. We find collective motion can emerge spontaneously when individuals act as sensory inputs to each other's networks, but only if individuals employ allocentric bearings to neighbors. Rapid switching between both representations can, however, enhance coordination. Collective motion can, therefore, emerge directly from navigational circuits, and thus may readily evolve, without requiring explicit alignment, or additional rules of interaction.

Fig. 1. Ring-attractor networks with an allocentric and an egocentric representation of space.

A Individuals are equipped with a ring-attractor network in which neurons are arranged on a ring. Each neuron receives sensory input from the external world through a Gaussian receptive field centered on an angle α_i (with respect to the individual’s allocentric or egocentric reference frame) and encodes for movement along the same direction, α_i. Besides, neurons interact with other neurons via excitatory or inhibitory synapses, depending on their distance along the ring. B With an egocentric representation of space, the animal encodes directions with respect to a self-body coordinate (head direction), α_ego. Whereas, with an allocentric representation, directions towards targets are encoded via an allocentric frame of reference, α_allo = α_r + α_ego, where α_r is the direction of the individual’s body axis. Thus, with an allocentric representation, directions are independent of the agent’s body coordinate. C To model an allocentric representation of space, we assume the neural network (represented by only four circles for better visibility) encodes for directions in a world-centric reference frame, which does not rotate with the individual’s movement in space (as if it is anchored in the external world, using one or more external cues), such that, neuron i, encodes for a direction, 2π(i−1)/N_s with respect to a world-centric axis. In the egocentric case, the network’s reference frame is attached to the individual and rotates with the individual as the individual moves in space, such that neuron i encodes for a direction, 2π(i−1)/N_s, with respect to the animal’s body axis.

Fig. 2. Individual motion.

A–C The network activity as a function of time (i) and the resulting trajectories for egocentric ii and allocentric iii representation of space, for increasing values of β from the disordered phase (small β, A) to the ordered phase (large β, C) are shown. In the disordered phase, the agent exhibits a random walk, and no difference between an allocentric and an egocentric representation of space is observed (A). 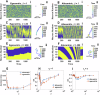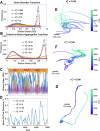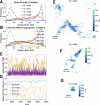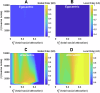As β increases, differences become apparent. An egocentric representation of space results in a more meandering motion (ii), and an allocentric representation leads to a more directed motion (iii). For larger values of β, corresponding to the highly ordered network activity (C), motion patterns with an egocentric representation of space correspond to circular orbits (ii), and for an allocentric representation, correspond to a straight line (iii). Parameter values: v₀ = 10, σ = 2π/N_s, h₀ = 0, h_b = 0, L = 1000, and N_s = 100.

Fig. 3. Individual information acquisition.

A–F The network activity as a function of time (i) and the resulting trajectories (ii) for egocentric and allocentric representations for increasing values of β is shown. For too small β, for both egocentric and allocentric representations of space, the agent only exhibits random and slow movement. Above the order-disorder transition, the agent moves towards the target. For smaller values of β, noise drives transitions between states, which facilitate information acquisition by endowing the agent with flexibility. In the ordered phase, external stimuli elicit distinct network activities for allocentric and egocentric representations of space. With an allocentric representation, external stimuli can lead to the formation of damped traveling waves corresponding to spiral motion toward the target (with more stability for larger values of β). For too large β, trajectories intermittently veer away from the target. With an egocentric representation, external stimuli help stabilize a bump of activity, allowing agents to remain stationary once it has found the target. G The agent’s decision-making time in finding a stationary target, defined as the time needed for the agent to reach close proximity of the target (5 dimensionless units), is plotted as a function of β. Decision-making time is minimized in the ordered phase. An allocentric representation can improve the decision-making speed in the effective decision-making region. H, I The time average distance of the agent to the target, normalized by the arena size L = 1000, d/L, as a function of β for both allocentric and egocentric representations and for different target speeds, is plotted. For a stationary or slowly moving target, an egocentric representation is beneficial by allowing the agent to stay stationary once it finds the target. However, for larger target speeds, an allocentric representation improves information acquisition by facilitating the tracking of a rapidly moving target. In both cases, the information acquisition optimizes in the ordered phase but is close to the critical point. Parameter values: v₀ = 10, σ = 2π/N_s, L = 1000, h₀ = 0.0025, and h_b = 0. A–F N_s = 100, and in G–I N_s = 400.

Fig. 4. Collective behavior of agents with egocentric and allocentric representation of space.

A, B Global order (GO in A), defined as the angular order parameter (AOP), and Local Order (LO in B), defined as the topological vectorial order parameter (VOP), in groups of 80 agents with an egocentric representation of space are color plotted as a function of the network inverse temperature, β, and total social attraction, $h_{\mathrm{t}}^{\mathrm{s}}$. For a too small social attraction, the agents move independently. As the social attraction increases, local order increases but not global order, indicating the onset of an aggregation phase where agents aggregate in a stationary dense group. C, D The global (C) and local (D) order in groups of 80 agents with allocentric representation of space as a function of the network inverse temperature, β, and total social attraction, $h_{\mathrm{t}}^{\mathrm{s}}$, are color plotted. The system shows three distinct phases: disordered motion for small $h_{\mathrm{t}}^{\mathrm{s}}$, collective motion with high local and global order, and aggregation phase with low global but high local order. Local order is minimized close to the phase transition between collective motion and aggregation due to the strong fission-fusion dynamics leading to explosive movement of the densely packed group. Parameter values: N_s = 100, v₀ = 10, σ = 2π/N_s, h_b = 0, N = 80, and L = 1000.

Fig. 5. Phase transitions in collectives with an egocentric representation of space.

A, B The distributions of global order (GO) and local order (LO) in groups of various sizes of agents with egocentric representation of space for different values of total social attraction, $h_{\mathrm{t}}^{\mathrm{s}}$, are plotted. By increasing $h_{\mathrm{t}}^{\mathrm{s}}$, the system shows a phase transition from a disordered phase, where individuals move independently, to an aggregation phase, where individuals form aggregates, and no collective motion is observed. While GO takes a small value and does not show sensitivity to social attraction (indicating no collective motion exists), LO shows bimodality close to the order-disorder transition, indicating a discontinuous transition from the disordered phase with low LO to the aggregation phase with high LO. C, D Snapshots of the collective behavior in the ordered phase are shown. For large β (low network noise), in the ordered phase, agents form an almost stationary circular pack of densely aggregated agents. For smaller β, the pack’s radius increases, and agents perform a random walk-like movement within the pack. C shows a snapshot of a dense pack for large β and D shows trajectories of the individuals within a pack for smaller values of β. Local order is high in both cases. Parameter values: N_s = 100, v₀ = 10, σ = 2π/N_s, h_b = 0, β = 400, N = 80, and L = 1000.

Fig. 6. Collective behavior in small groups of agents with an allocentric representation of space.

A, B The distribution of GO and LO in groups of various sizes of agents with allocentric representation of space close to the order-disorder transition (A) and close to the collective motion-aggregation phase transition (B). In both cases, the distribution shows bimodality, signaling a discontinuous pseudo-phase transition in small system sizes. C, D GO and mean distance between all pairs normalized by space size, L, as a function of time for different values of total social attraction are plotted. For small social attraction, the system shows intermittency between high and low order, and for larger social attraction, intermittency between ordered motion and aggregation is observed. E–G Example snapshots of motion patterns from the Supplementary Videos for some values of $h_{\mathrm{t}}^{\mathrm{s}}$ shown in (A, B). In the collective motion phase, the system shows a rich set of motion patterns, including swirling in circular orbits (E), or in coil-shaped orbits (F), fission-fusion dynamics, and intermittency between highly ordered motion and aggregation (G). Parameter values: N_s = 100, v₀ = 10, σ = 2π/N_s, h_b = 0, β = 400, N = 10, and L = 1000.

Fig. 7. Collective behavior in large groups of agents with allocentric representation of space.

A, B The distribution of GO (AOP) and LO (normalized topological VOP) in groups of various sizes of agents with an allocentric representation of space close to the order-disorder transition (A) and close to the collective motion-aggregation phase transition (B). Both phase transitions tend to a continuous phase transition, indicated by large fluctuations and a broad distribution of the order parameter, as group size increases. C, D Global order (GO) and mean distance between all pairs normalized by space size, L, as a function of time for different values of total social attraction are plotted. The system shows intermittency between high and low orders resulting from transitions between different motion patterns and strong fission-fusion dynamics. E–G Example snapshots of motion patterns from the Supplementary Videos for some values of $h_{\mathrm{t}}^{\mathrm{s}}$ shown in A, B. In the collective motion phase, the system shows a rich set of motion patterns, including flocking (E), sudden direction change and fission-fusion dynamics (F), and intermittency between highly ordered motion and aggregation leading to explosive movement with low local order (G). Parameter values: N_s = 100, v₀ = 10, h_b = 0, σ = 2π/N_s, β = 400, N = 320, and L = 1000.

Fig. 8. Cognitive representation of collective motion.

A A snapshot of the collective motion in a population of 80 agents is shown. The population can be decomposed into subgroups of synchronized agents. B and C The motion pattern (B) and the neural activity (C) of a subgroups of three coherently moving agents among the 80 agents presented in (A) are shown. The coordinated movement of the agents results from the synchronization of their neural dynamics. D, E An example of fission-fusion and leader-follower dynamics is shown. In the beginning, agents 4–6 are synchronized and move together, and agents 7 and 8 move together. When these two groups come into close proximity, at around timestep 1000, agent 6 changes its mind and joins agents 6 and 7. Consequently, its neural activity becomes synchronized with agents 7 and 8. Around time 1050, a sudden direction change by agent 6 drives a sudden direction change in agent 8, followed by a similar behavior of agent 7. Parameter values: N_s = 100, v₀ = 10, σ = 2π/N_s, h_b = 0, β = 400, N = 80, and L = 1000.

Fig. 9. Collective behavior in the neural field model.

A, B Global order (GO in A), defined as the angular order parameter (AOP), and Local Order (LO in B), defined as the topological vectorial order parameter (VOP), in groups of 80 agents with an egocentric representation of space are color plotted as a function of the network inverse temperature, β, and total social attraction, $h_{\mathrm{t}}^{\mathrm{s}}$. Both local and global order remain small, indicating collective movement is not observed with an egocentric representation of space. C, D The same quantities for an allocentric representation of space are plotted. Similarly to the spin system model, the system shows disordered motion for small $h_{\mathrm{t}}^{\mathrm{s}}$, collective motion with high local and global order, and aggregation phase with low global but high local order. Parameter values: N_s = 100, ν = 0.5, v₀ = 0.05, σ = 0.4, h_b = 0, N = 80, Δt = 0.3, and L = 1000.

Fig. 10. Switching between allocentric and egocentric reference frames.

Global order (A) and local order (B) in the neural field model, where individuals randomly switch between allocentric and egocentric representations of space, are color plotted as a function of $h_{\mathrm{t}}^{\mathrm{s}}$ and the probability of being in the egocentric state, ω. A certain rate of random switch between allocentric and egocentric representations can increase global and local order by stabilizing highly ordered collective motion at the expense of reduced complexity of the motion patterns. C, D show snapshots of collective motion close to the maximal order region when individuals possess a purely allocentric representation of space (C) and when they switch at a rate close to the rate leading to maximal order (D). Parameter values: N_s = 100, ν = 0.5, v₀ = 0.05, σ = 0.4, h_b = 0, N = 80, Δt = 0.3, β = 1000, and L = 1000.