Statistical Inference for the Evolutionary History of Cancer Genomes
- PMID: 41098675
- PMCID: PMC12519734
- DOI: 10.1214/19-sts7561
Statistical Inference for the Evolutionary History of Cancer Genomes
Abstract
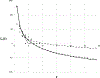
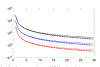
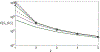
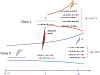
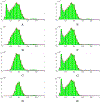
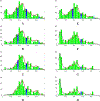
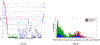
Recent years have seen considerable work on inference about cancer evolution from mutations identified in cancer samples. Much of the modeling work has been based on classical models of population genetics, generalized to accommodate time-varying cell population size. Reverse-time, genealogical views of such models, commonly known as coalescents, have been used to infer aspects of the past of growing populations. Another approach is to use branching processes, the simplest scenario being the classical linear birth-death process. Inference from evolutionary models of DNA often exploits summary statistics of the sequence data, a common one being the so-called Site Frequency Spectrum (SFS). In a bulk tumor sequencing experiment, we can estimate for each site at which a novel somatic point mutation has arisen, the proportion of cells that carry that mutation. These numbers are then grouped into collections of sites which have similar mutant fractions. We examine how the SFS based on birth-death processes differs from those based on the coalescent model. This may stem from the different sampling mechanisms in the two approaches. However, we also show that despite this, they are quantitatively comparable for the range of parameters typical for tumor cell populations. We also present a model of tumor evolution with selective sweeps, and demonstrate how it may help in understanding the history of a tumor as well as the influence of data pre-processing. We illustrate the theory with applications to several examples from The Cancer Genome Atlas tumors.
Keywords: Cancer evolution; birth-death processes; bulk sequencing; clonal selection; coalescents; ploidy; site frequency spectrum; tumor heterogeneity.
Figures
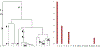
References
-
- Abramowitz M and Stegun IA (1964). Handbook of Mathematical Functions. Applied Mathematics Series 55. National Bureau of Standards.
-
- Cheek D and Antal T (2018). Mutation frequencies in a birth-death branching process. Ann. Appl. Probab. 28 3922–3947. MR3861830 10.1214/18-AAP1413 - DOI
-
- Dinh KN, Jaksik R, Kimmel M, Lambert A and Tavaré S (2020). Supplement to “Statistical inference for the evolutionary history of cancer genomes.” 10.1214/19-STS7561SUPP. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
