Optimization by decoded quantum interferometry
- PMID: 41125774
- PMCID: PMC12545177
- DOI: 10.1038/s41586-025-09527-5
Optimization by decoded quantum interferometry
Abstract
Achieving superpolynomial speed-ups for optimization has long been a central goal for quantum algorithms1. Here we introduce decoded quantum interferometry (DQI), a quantum algorithm that uses the quantum Fourier transform to reduce optimization problems to decoding problems. When approximating optimal polynomial fits over finite fields, DQI achieves a superpolynomial speed-up over known classical algorithms. The speed-up arises because the algebraic structure of the problem is reflected in the decoding problem, which can be solved efficiently. We then investigate whether this approach can achieve a speed-up for optimization problems that lack an algebraic structure but have sparse clauses. These problems reduce to decoding low-density parity-check codes, for which powerful decoders are known2,3. To test this, we construct a max-XORSAT instance for which DQI finds an approximate optimum substantially faster than general-purpose classical heuristics, such as simulated annealing. Although a tailored classical solver can outperform DQI on this instance, our results establish that combining quantum Fourier transforms with powerful decoding primitives provides a promising new path towards quantum speed-ups for hard optimization problems.
© 2025. The Author(s).
Conflict of interest statement
Competing interests: Google has filed a patent application pertaining to the DQI algorithm, on which S.P.J. is the inventor.
Figures
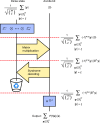
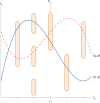
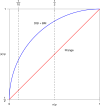
References
-
- Abbas, A. et al. Challenges and opportunities in quantum optimization. Nat. Rev. Phys.6, 718–735 (2024).
-
- Gallager, R. G. Low-Density Parity-Check Codes (MIT, 1963).
-
- Richardson, T. J. & Urbanke, R. L. The capacity of low-density parity-check codes under message-passing decoding. IEEE Trans. Inf. Theory47, 599–618 (2001).
-
- Trevisan, L. in Paradigms of Combinatorial Optimization: Problems and New Approaches 2nd edn (ed. Paschos, V. Th.) Ch. 13 (Wiley, 2014).
-
- Ajtai, M., Kumar, R. & Sivakumar, D. A sieve algorithm for the shortest lattice vector problem. In Proc. 33rd Annual ACM Symposium on Theory of Computing 601–610 (ACM, 2001).
LinkOut - more resources
Full Text Sources

