Mapping Incidence and Prevalence Peak Data for SIR Modeling Applications
- PMID: 41165884
- PMCID: PMC12575469
- DOI: 10.1007/s00285-025-02299-6
Mapping Incidence and Prevalence Peak Data for SIR Modeling Applications
Abstract
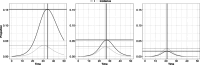
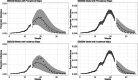
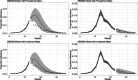
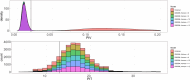
Infectious disease modeling and forecasting have played a key role in helping assess and respond to epidemics and pandemics. Recent work has leveraged data on disease peak infection and peak hospital incidence to fit compartmental models for the purpose of forecasting and describing the dynamics of a disease outbreak. Incorporating these data can greatly stabilize a compartmental model fit on early observations, where slight perturbations in the data may lead to model fits that forecast wildly unrealistic peak infection. We introduce a new method for incorporating historic data on the value and time of peak incidence of hospitalization into the fit for a Susceptible-Infectious-Recovered (SIR) model by formulating the relationship between an SIR model's starting parameters and peak incidence as a system of two equations that can be solved computationally. We demonstrate how to calculate SIR parameter estimates - which describe disease dynamics such as transmission and recovery rates - using this method, and determine that there is a noticeable loss in accuracy whenever prevalence data is misspecified as incidence data. To exhibit the modeling potential, we update the Dirichlet-Beta State Space modeling framework to use hospital incidence data, as this framework was previously formulated to incorporate only data on total infections. This approach is assessed for practicality in terms of accuracy and speed of computation via simulation.
Keywords: Compartmental Models; Disease Forecasting; Hospital Incidence; Prevalence.
© 2025. This is a U.S. Government work and not under copyright protection in the US; foreign copyright protection may apply.
Conflict of interest statement
Declarations. Competing Interests: The authors have no non-financial or other financial competing interests to declare that are relevant to the content of this article other than the aforementioned declared funding sources. Code Availability: All software used to perform the simulations and studies in this paper are publicly available at https://github.com/lanl/precog .
Figures


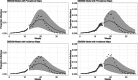
References
-
- Abbey H ( 1952) An examination of the reed-frost theory of epidemics. Human Biology 24( 3), 201– 233. Accessed 2024-03-21 - PubMed
-
- Anderson RM (1988) The role of mathematical models in the study of hiv transmission and the epidemiology of aids. J Acquir Immune Defic Syndr 1(3):241–256 - PubMed
-
- Burr T, Chowell G (2006) Observation and model error effects on parameter estimates in susceptible-infected-recovered epidemiological models. Far East Journal of Theoretical Statistics 19(2):163–183
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

