Simulation-Based Spatially Explicit Close-Kin Mark-Recapture
- PMID: 41195462
- PMCID: PMC12632178
- DOI: 10.1111/1755-0998.70074
Simulation-Based Spatially Explicit Close-Kin Mark-Recapture
Abstract
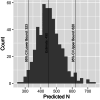
Estimating the size of wild populations is a critical priority for ecologists and conservation biologists, but tools to do so are often labour intensive and expensive. A promising set of newer approaches are based on genetic data, which can be cheaper to obtain and less invasive than information from more direct observation. One of these approaches is close-kin mark-recapture (CKMR), a type of method that uses genetic data to identify kin pairs and estimates population size from these pairs. Although CKMR methods are promising, one limitation to using them more broadly is a lack of CKMR models that can deal with spatially structured populations and spatial heterogeneity in sampling. In this paper, we introduce a spatially explicit approach to CKMR that uses individual-based simulation in concert with a deep convolutional neural network to estimate population sizes. Using simulations, we show that our method, CKMRnn, is highly accurate, even in the face of spatial heterogeneity in sampling and spatial population structure, and demonstrate that it can account for potential confounders such as unknown population histories. Finally, to demonstrate the accuracy of our method in an empirical system, we apply CKMRnn to data from a Ugandan elephant population, and show that point estimates from our method recapitulate those from traditional estimators but that the confidence interval on our estimator is approximately 30% narrower.
© 2025 The Author(s). Molecular Ecology Resources published by John Wiley & Sons Ltd.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures
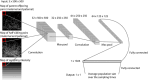


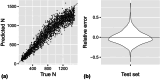
Update of
-
Simulation-based spatially explicit close-kin mark-recapture.bioRxiv [Preprint]. 2025 Jun 3:2025.05.31.656892. doi: 10.1101/2025.05.31.656892. bioRxiv. 2025. Update in: Mol Ecol Resour. 2026 Jan;26(1):e70074. doi: 10.1111/1755-0998.70074. PMID: 40502080 Free PMC article. Updated. Preprint.
References
-
- Armbruster, P. , and Lande R.. 1993. “A Population Viability Analysis for African Elephant (<styled-content style="fixed-case"> Loxodonta Africana </styled-content>): How Big Should Reserves Be?” Conservation Biology 7, no. 3: 602–610.
-
- Athira, T. K. , and Vidya T. N. C.. 2021. “Elephant Social Systems: What Do We Know and How Have Molecular Tools Helped?” Journal of the Indian Institute of Science 101, no. 2: 257–278. 10.1007/s41745-021-00226-4. - DOI
-
- Babyn, J. , Ruzzante D., Bravington M., and Mills Flemming J.. 2024. “Estimating Effective Population Size Using Close‐Kin Mark–Recapture.” Methods in Ecology and Evolution 15, no. 11: 2059–2073. 10.1111/2041-210X.14419. - DOI
-
- Baillargeon, S. , and Rivest L.‐P.. 2007. “Rcapture: Loglinear Models for Capture–Recapture in R.” Journal of Statistical Software 19: 1–31. 10.18637/jss.v019.i05. - DOI
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

