Free space few-photon nonlinearity in critically coupled polaritonic metasurfaces

Abstract

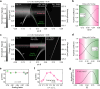
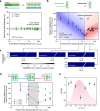
Few-photon optical nonlinearity in planar solid-state systems is challenging yet crucial for quantum and classical optical information processing. Polaritonic nonlinear metasurfaces have emerged as a promising candidate to push the photon number down - but have often been hindered by challenges like the poor photon-trapping efficiency and lack of modal overlap. Here, we address these issues in a self-hybridized perovskite metasurface through critical coupling engineering, and report strong polaritonic nonlinear absorption at an ultra-low incident power density of only 519 W/cm², with an estimated photon number of 6.12 per cavity lifetime. Taking advantage of a quasi-bound-state-in-the-continuum design with asymmetry-controlled quality-(Q)-factor, we systematically examine the Q-dependent device nonlinearity and determine the optimal cavity critical coupling condition. With the optimized device, we demonstrate at 6 Kelvin a tunable nonlinear response from reverse saturable absorption to saturable absorption at varying pump powers, with a maximal effective nonlinear absorption coefficient up to 29.4 ± 5.8 cm/W at 560 nm wavelength. In addition, the cavity-exciton detuning dependent device response is analyzed and well explained by a phase-space-filling model, elucidating the underlying physics and the origin of giant nonlinearity. Our study paves the way towards practical flat nonlinear optical devices with large functional areas and massive parallel operation capabilities.

Fig. 1. Engineering cavity critical coupling in perovskite metasurfaces based on quasi-bound state in the continuum (quasi-BIC).

a Schematic of the perovskite metasurface in a rod-type symmetry-protected quasi-BIC design. Underneath a PMMA superstrate, a periodic array of FAPbBr₃ perovskite nano-rods is embedded in the SiO₂ substrate. The geometrical unit cell parameters include the lengths of two asymmetric rods L = 252.5 nm and $L-△L=\left(1-\alpha \right)L$, respectively, the width of the rods W = 112.5 nm, the distance between two rods D = 112.5 nm, the PMMA thickness t_PMMA = 50 nm, the rod thickness t_perovskite = 60 nm, and the period P_X = P_Y = 475 nm. An asymmetry parameter $\alpha =△L/L$ between 0 and 1 is applied to tune the cavity intrinsic quality factor Q_int. A multiplicative scaling factor is applied on the lateral geometrical parameters only (thicknesses unchanged) to tune the resonance wavelength. b Top, Tuning Q_int via different $\alpha$ values to match the material background loss Q_bg for the cavity critical coupling. Middle and Bottom, Simulated electric field enhancement inside the perovskite rods as a function of applied asymmetry parameter $\alpha$ when the non-exciton background loss of perovskite is considered (Middle) and not considered (Bottom). A hypothetical perovskite dielectric function with the exciton resonance turned off is applied (see Supplementary Note 1). Scaling factor = 0.76. c Simulated electric (left) and magnetic (right) field profiles at the quasi-BIC resonance of a perovskite metasurface with $\alpha$ = 0.30 and scaling factor = 0.76. The arrows show the directions of field vectors. d, e Simulated transmittance spectra of quasi-BIC perovskite metasurfaces under normal incidence as a function of (d) scaling factor and (e) asymmetry parameter $\alpha$, respectively. The exciton resonance is turned off.

Fig. 2. Towards large polaritonic nonlinearity under photon-exciton strong coupling.

a Left, Experimentally measured energy-momentum photoluminescence (PL) spectrum (at 6 K) and simulated absorption (Abs) spectrum of a self-hybridized perovskite metasurface with $\alpha$ = 0.30 and scaling factor = 0.76, showing the strong coupling between the photonic cavity mode and perovskite excitons. LP, lower polariton branch. Right, Simulated reflectance (Reflec) spectrum of a hypothetical perovskite metasurface of the same geometrical parameters but with the exciton resonance turned off (see Supplementary Note 1). b Fitted Hopfield coefficients as a function of momentum for the studied device in (a). A coupled oscillator model is applied to fit the energy-momentum PL spectrum (see “Methods” and Supplementary Note 3). The shaded green and pink backgrounds denote photon-like and exciton-like fractions, respectively. c, d The same as (a, b) respectively, but for another perovskite metasurface with $\alpha$ = 0.30 and scaling factor = 0.88. e Fitted coupling strengths $g$ of devices with a fixed asymmetry parameter $\alpha$ = 0.30 and different scaling factors. f Fitted coupling strengths $g$ of devices with a fixed scaling factor = 0.88 and different asymmetry parameters $\alpha$, revealing a maximum at the cavity critical coupling condition. g Theoretical total polaritonic nonlinearity strength as a function of Hopfield coefficient |C| that represents the proportion of photon in the polariton state. |C| can be tuned in the momentum space as shown in (b, d).

Fig. 3. Low-photon-number tunable nonlinear absorption of self-hybridized perovskite exciton-polaritons enabled by cavity critical coupling engineering.

a Power-density-dependent reflection of a bare perovskite thin film on SiO₂ substrate and encapsulated by PMMA, showing a repeatable linear optical response. The insets on top are the schematics of a bare perovskite thin film and a patterned perovskite metasurface for comparison in optical response. b Power-density-dependent relative reflection (compared to bare perovskite in (a)) of polaritons in a self-hybridized perovskite metasurface with $\alpha$ = 0.30 and scaling factor = 0.88. The shaded blue and red areas highlight two different regimes with nonlinear optical responses of reverse saturable absorption (RSA) and saturable absorption (SA), respectively. The switching from RSA to SA can be controlled by incident power density. The schematics on top conclude an incident-power-dependent functional switch from ‘reflectance allowed’ to ‘reflectance forbidden’, with potential applications in nonlinear optical switches. c Examples of measured energy-momentum reflection spectra at different power densities, where the polariton reflection data in (b) are extracted from. The dip value and four nearest pixels are considered. The error bar shows the standard deviation. d Power-density-dependent polariton reflection of different devices deviating from the optimal cavity critical coupling condition, showing the nonlinear optical response as a function of metasurface asymmetry parameters $\alpha$. A parameter ∆R (gray-shaded area) is defined to evaluate the nonlinearity strength. e ∆R as a function of metasurface asymmetry parameters $\alpha$. The pink-shaded background reproduces the trend of fitted coupling strength $g$ as a function of $\alpha$ in Fig. 2f as a reference. The maximum nonlinearity is achieved at the cavity critical coupling condition.

Fig. 4. Dependence of polaritonic nonlinearity strengths on Hopfield coefficients.

a Power-density-dependent relative reflection (compared to bare perovskite thin film) of the polaritons of different wavelengths. The same self-hybridized perovskite metasurface with $\alpha$ = 0.30 and scaling factor = 0.88 (at cavity critical coupling) in Fig. 3b is studied. Along the polariton branch, each polariton wavelength corresponds to a specific momentum value and Hopfield coefficient |C| (see Fig. 2d and Supplementary Fig. 10). When extracting the reflection data from energy-momentum spectra, the dip value and four nearest pixels are considered. The error bar shows the standard deviation. b The same data in (a) but the X axis is converted from pulse power density to polariton density. Details of the conversion calculation can be found in Supplementary Note 6. In (a, b), the transition thresholds from RSA to SA are defined as P_threshold and D_threshold, respectively. c P_threshold as a function of Hopfield coefficient |C | , evaluating the total polaritonic nonlinearity strength. A smaller P_threshold suggests more significant nonlinearity. d Calculated conversion ratio as a function of |C | . e D_threshold as a function of |C | , evaluating the single polariton nonlinearity strength. A smaller D_threshold suggests more significant nonlinearity. f–h Theoretical expectation of (f) total polaritonic nonlinearity strength, (g) photon-to-polariton conversion ratio, and (h) single polariton nonlinearity strength, as a function of |C | , according to the phase-space filling mechanism. The shaded green and pink backgrounds denote photon-like and exciton-like fractions, respectively.