Orthonormal pairwise logratio selection (OPALS) algorithm for compositional data analysis in high dimensions

Abstract

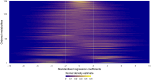
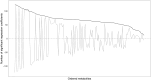
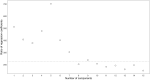
Summary: In the analysis of compositional data, the most fundamental information is conveyed by the pairwise logratios between components. While logratio coordinate representations, such as balances and pivot coordinates, are widely used to aggregate such information into higher-level relationships, there are instances where a fine-grained representation using all pairwise logratios can be advantageous. Performing this within an orthonormal (or orthogonal) logratio coordinate framework becomes particularly challenging for high-dimensional compositions, since a composition with D parts results in $D(D-1)/2$ pairwise logratios (excluding reciprocals). This work presents an efficient algorithm (OPALS) based on Latin squares theory to obtain all orthonormal pairwise logratios from just $D-1$ logratio coordinate systems. Thus, the computational burden associated with using such representation for data analysis and modelling in high dimensions is notably alleviated, or even made feasible. Moreover, the relationship between estimates from orthonormal pairwise logratios and ordinary pivot coordinates is discussed in the context of regression and classification analysis.

Availability and implementation: The OPALS algorithm is described in detail in this article and can be implemented directly from the provided methodology. The performance and properties of the method are illustrated through two examples using contemporary molecular biology data.

Figure 1.

Schematic comparison of the bpc and OPALS approaches to obtain orthonormal pairwise logratios from a 6-part composition. At the top, the step from $D=6$ parts to $D(D-1)/2$ pairwise logratios is illustrated. Then, the orthonormal coordinate systems required by each approach to cover all those pairwise logratios are represented (15 in the bpc case and 5 in the OPALS case).

Figure 2.

Ratios between coefficients PLS regression models based on ordinary and backwards pivot coordinates for various numbers of observations and compositional parts, with increasing numbers of PLS components. (A) Scenario 100 × 50, (B) Scenario 200 × 50, (C) Scenario 100 × 150, (D) Scenario 200 × 150, (E) Scenario 100 × 450, (F) Scenario 200 × 450.

Figure 3.

Heatmap of the empirical distributions of standardized PLS regression coefficient estimates associated to each metabolite, ordered according to number of significant coefficients. The vertical lines indicate 2.5% and 97.5% quantile cut-off limits used to determine statistical significance at the 5% level.

Figure 4.

Total number of significant standardized PLS regression coefficients associated to each metabolite (black line) and difference between number of positive and negative ones amongst them (grey line). Metabolites represented on the x-axis in decreasing order according to total number of significant coefficients associated to them.

Figure 5.

Ratios between PLS-DA model coefficients based on ordinary and backward pivot coordinates for increasing numbers of PLS components from the liver cirrhosis microbiome data example. The horizontal dashed line indicates the D/2 threshold.