Instability by Extension of an Elastic Nanorod

Abstract

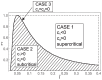
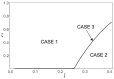
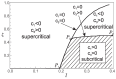
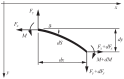
The static stability of an elastic, incompressible nanorod subjected to an extensional force is analyzed. The force is applied to a rigid rod that is welded to the free end of the nanorod. The material behavior of the nanorod is described using a two-phase local/nonlocal stress-driven model. Mathematically, the problem is formulated as a system of nonlinear differential equations suitable for nonlinear analysis. For the analysis, the Liapunov-Schmidt method is employed. Depending on a geometric parameter (the length of the rigid rod) and nonlocal parameters (the small length-scale parameter and the phase parameter), the buckling load and post-buckling behavior of the nanorod are determined. The results show that the nonlocal effect increases the buckling load, indicating a stiffening effect. An increase in the length of the rigid rod decreases the buckling load. Regarding the post-buckling behavior, it is shown that both supercritical and subcritical bifurcations can occur, depending on the values of the geometric and nonlocal parameters. The occurrence of a subcritical bifurcation, which is highly undesirable in real-world constructions, is a novel effect not observed in the classical Bernoulli-Euler theory.

Keywords: Liapunov–Schmidt method; buckling; extension; nanorod; post-buckling; two-phase local/nonlocal stress-driven model.

Figure 7

Influence of the dimensionless small length-scale parameter $\overline{l}$ and the phase parameter $\zeta$ for $\overline{a}=0.05$ on: (a) regions (Case 1, Case 2, Case 3) corresponding to the three characteristic equations that determine the buckling loads; (b) the values of coefficients $c_1$ and $c_3$ in the bifurcation equation; (c) the type of bifurcation.

Figure 8

Influence of the dimensionless small length-scale parameter $\overline{l}$ and the phase parameter $\zeta$ for $\overline{a}=0.25$ on: (a) regions (Case 1, Case 2, Case 3) corresponding to the three characteristic equations that determine the buckling loads; (b) the values of coefficients $c_1$ and $c_3$ in the bifurcation equation; (c) the type of bifurcation.

Figure 9

Influence of the dimensionless small length-scale parameter $\overline{l}$ and the phase parameter $\zeta$ for $\overline{a}=0.48$ on the regions (Case 1, Case 2, Case 3) corresponding to the three characteristic equations that determine the buckling loads.

Figure 10

Influence of the dimensionless small length-scale parameter $\overline{l}$ and the phase parameter $\zeta$ for $\overline{a}=0.75$ on the regions (Case 1, Case 2, Case 3) corresponding to the three characteristic equations that determine the buckling loads.

Figure 11

Influence of the dimensionless small length-scale parameter $\overline{l}$ and the phase parameter $\zeta$ for $\overline{a}=0.48$ on: (a) the values of the coefficients $c_1$ and $c_3$ in the bifurcation equation; (b) the type of bifurcation.

Figure 1

A nanorod loaded by an extensive force P.

Figure 2

Contact forces and couples acting on an elementary part of the nanorod.

Figure 3

The dependence of the buckling load ${\lambda }_{cr}$ on the dimensionless small length-scale parameter $\overline{l}$ and the phase parameter $\zeta$ in the case of $\overline{a}=0.05$.

Figure 4

The dependence of the buckling load ${\lambda }_{cr}$ on the dimensionless small length-scale parameter $\overline{l}$ and the phase parameter $\zeta$ in the case of $\overline{a}=0.25$.

Figure 5

The dependence of the buckling load ${\lambda }_{cr}$ on the dimensionless small length-scale parameter $\overline{l}$ and the phase parameter $\zeta$ in the case of $\overline{a}=0.48$.

Figure 6

The dependence of the buckling load ${\lambda }_{cr}$ on the dimensionless small length scale parameter $\overline{l}$ and the phase parameter $\zeta$ in the case of $\overline{a}=0.75$.