Distributional bias compromises leave-one-out cross-validation

Abstract

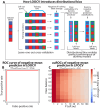
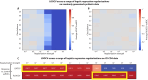
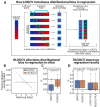
Cross-validation is a common method for evaluating machine learning models. "Leave-one-out cross-validation," in which each data instance is used to test a model trained on all other instances, is often used in data-scarce regimes. As common metrics such as the R² score cannot be calculated for a single prediction, predictions are commonly aggregated across folds for performance evaluation. Here, we prove that this creates "distributional bias": a negative correlation between the average label of each training fold and the label of its corresponding test instance. As machine learning models tend to regress to the mean of their training data, this bias tends to negatively affect performance evaluation and hyperparameter optimization. We demonstrate that distributional bias exists across diverse tasks, models, and evaluation approaches, and can bias against stronger regularization. To address it, we developed a generalizable rebalanced cross-validation that is robust to distributional bias in both classification and regression, and demonstrates improved performance in simulations, machine learning benchmarks, and several published analyses.

Fig. 1.. Distributional bias leaks the test set label in LOOCV.

(A) Illustration of how distributional bias occurs in LOOCV. When a held-out data instance belongs to either class, the class average of the remaining dataset shifts by $\frac{1}{N-1}$ in the other direction. As a result, a dummy predictor that returns the negative of the average training class label would produce predictions that are perfectly correlated with the actual labels. (B) Receiver operator characteristic (ROC) curve for this dummy negative-mean predictor. The auROC is 1 under any scenario regardless of the underlying data. (C) Heatmap showing the average auROC of the same dummy negative-mean predictor under different class balances and P-left-out schema on randomly generated labels, with resulting auROCs consistently over the expected null auROC of 0.5. Each cell in the heatmap shows the results of 100 independent simulations.

Fig. 2.. Distributional bias produces results worse than a random guess on random data.

All plots pertain to LOOCV and LPOCV analyses of logistic regression models on randomly generated data and labels. The auROC in this setting should be 0.5 in any fair evaluation. In (A) and (B), one point corresponds to one simulated dataset; in (C), one cell corresponds to 10 simulations. (A) Boxplots of auROCs for a standard LOOCV implementation across different underlying class balances. Resulting auROCs are consistently less than 0.5 (aggregated P < 0.001 via a single one-sample t test). (B) Boxplots of auROCs on stratified leave-5-out cross-validation across different class balances. When the class balances can be precisely captured with five samples (e.g., class balance of 0.2), the distribution of resulting auROCs has a mean that is not significantly different from 0.5 (one-sample t test versus 0.5 P = 0.59). Otherwise, under-evaluation of performance is evident (e.g., for class balance of 0.1). (C) Heatmap of average auROCs on stratified LPOCV for Ps ranging from 1 to 10 and for different class balances. Results demonstrate that the effect of distributional bias, observed as auROCs below 0.5, is smaller the closer the stratification enabled by P and the class balance is to optimal stratification. Box, IQR; line, median; whiskers, nearest point to 1.5*IQR.

Fig. 3.. Rebalancing training data through subsampling avoids distributional bias.

(A) Illustration of our proposed rebalanced LOOCV (RLOOCV) for classification. For each test instance (or fold), we remove from the training set a data instance with the opposite label such that the training set’s label mean is constant across all folds. This can be accomplished by randomly removing a single training instance with a label opposite that of the test instance. (B) ROC curve of the negative-mean predictor (similar to Fig. 1B) evaluated via RLOOCV, which resulted in an auROC of 0.50 (the expected result for an evaluation of a dummy predictor). (C) Boxplots (box, IQR; line, median; whiskers, nearest point to 1.5*IQR) of auROCs of a logistic regression model trained on randomly generated data, similar to Fig. 2A, but evaluated with RLOOCV. The resulting auROCs are not consistently higher or lower than the expected 0.5 (P = 0.84 via a single aggregated one-sample t test).

Fig. 4.. Correcting distributional bias with RLOOCV improves performance evaluation of published predictive models.

(A) auROCs (y axis) of L²-regularized logistic regression models trained in cross-validation on multiple classification benchmarks from UCIMLR (Materials and Methods). “PCA” denotes results of models that were provided only with the first two principal components, which are less expressive and have a stronger tendency to regress to the mean. (B to E) ROC curves comparing the performance of published models evaluated with LOOCV with the same models evaluated using our rebalancing approach (RLOOCV) over 10 bootstrap runs. Tasks include predicting preterm birth from vaginal microbiome samples using logistic regression (40, 41) (B); predicting complications from immune checkpoint blockade therapy using T cell measurements (42), also using logistic regression (C); and predicting chronic fatigue syndrome from standard blood test measurements (45) using gradient boosted regression (D) and XGBoost (E). Across all cases, we observed a small but consistent improvement from RLOOCV (Fisher’s multiple comparison of DeLong tests P = 0.015 across all four evaluations). Shaded areas represent 95% confidence intervals.

Fig. 5.. Distributional bias and LOOCV favor weaker regularization.

(A and B) Heatmaps pertain to analyses of logistic regression models on randomly generated data and labels, where the auROC should be 0.5 in any fair evaluation. (A) Average auROCs evaluated with LOOCV across varying L² regularization strength and class balances, which are consistently less than 0.5 (P < 0.001 via one-sample t test across all values). (B) Same heatmap as in (A), but with RLOOCV. Resulting auROCs are not consistently higher or lower than 0.5 (Fisher’s combined probability test across six independent one-sample t tests versus 0.5 P = 0.23). (C) Heatmap showing the auROC obtained by logistic regression models classifying patients who experienced complications from immune checkpoint blockade therapy using T cell measurements (Materials and Methods). Different rows correspond to evaluation using LOOCV and RLOOCV, while different columns correspond to different regularization strengths. The optimal performance in each setup was obtained by RLOOCV. Additionally, the optimal performance under LOOCV was obtained with weaker regularization compared to evaluation with RLOOCV, suggesting that distributional bias can cause models tuned via LOOCV to be less regularized.

Fig. 6.. Distributional bias and RLOOCV generalize to regularization.

(A) Illustration of how distributional bias occurs in LOOCV in regression. For any held-out instance, the average of the remaining dataset shifts slightly in the other direction. As a result, a dummy predictor that returns the average training class label would produce predictions that are perfectly inversely correlated with the held-out labels. (B) Example of distributional bias manifesting in LOOCV of a simulated dataset (blue) and its absence in RLOOCV (orange). By selectively removing from the training dataset one additional data instance to shift the average as close as possible to the data average (black line), but not past it, we can alleviate the impact of distributional bias on the data. (C) Synthetic simulations in which all data features and labels are random (Materials and Methods), meaning that a correct evaluation should yield R² of 0. LOOCV evaluations of L²-regularized regression models yield median values less than 0 (one-sample t test versus 0 P = 7.1 × 10⁻⁸), while evaluations of RLOOCV demonstrate performances closer to the expected ground truth (Wilcoxon signed-rank P = 6.0 × 10⁻⁸ comparing LOOCV with RLOOCV; one-sample t test versus 0 P = 0.0017). (D) Evaluations of LOOCV and RLOOCV on regression tasks from UCIMLR (Materials and Methods), considering either all features or just the first two principal components. RLOOCV significantly outperforms LOOCV (Wilcoxon signed-rank P = 0.0039; P = 0.0024 for models run on the first two principal components).