A concurrent flow model for extraction during transcapillary passage
- PMID: 4608628
- PMCID: PMC3077802
- DOI: 10.1161/01.res.35.3.483
A concurrent flow model for extraction during transcapillary passage
Abstract
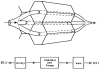
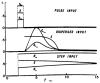
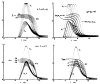
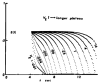
A model for capillary-tissue exchange in a uniformly perfused organ with uniform capillary transit times and no diffusional capillary interactions was designed to permit the exploration of the influences of various parameters on the interpretation of indicator-dilution curves obtained at the venous outflow following the simultaneous injection of tracers into the arterial inflow. These parameters include tissue geometric factors, longitudinal diffusion and volumes of distribution of tracers in blood and tissue, hematocrit, volumes of nonexchanging vessels and the sampling system, capillary permeability, P. capillary surface area, S, and flow of blood- or solute-containing fluid, Fs′. An assumption of instantaneous radial diffusion in the extravascular region is appropriate when intercapillary distances are small, as they are in the heart, or permeabilities are low, as they are for lipophobic solutes. Numerical solutions were obtained for dispersed input functions similar to normal intravascular dye-dilution curves. Axial extravascular diffusion showed a negligible influence at low permeabilities. The “instantaneous extraction” of a permeating solute can provide an estimate of PS/Fs′, the ratio of the capillary permeability–surface area product to the flow, when PS/Fs′ lies between approximately 0.05 and 3.0; the limits of the range depend on the extravascular volume of distribution and the influences of intravascular dispersion. The most accurate estimates were obtained when experiments were designed so that PS/Fs′ was between 0.2 and 1.0 or peak extractions were between 0.1 and 0.6.
Figures
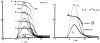
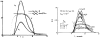

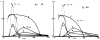
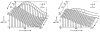
References
-
- Crone C. Permeability of capillaries in various organs as determined by use of the “indicator diffusion” method. Acta Physiol Scand. 1963;58:292–305. - PubMed
-
- Sangren WC, Sheppard CW. Mathematical derivation of the exchange of a labeled substance between a liquid flowing in a vessel and an external compartment. Bull Math Biophys. 1953;15:387–394.
-
- Renkin EM. Transport of potassium-42 from blood to tissue in isolated mammalian skeletal muscles. Am J Physiol. 1959;197:1205–1210. - PubMed
-
- Bassingthwaighte JB, Knopp TJ, Hazelrig JB. Concurrent flow model for capillary-tissue exchanges. In: Crone C, Lassen NA, editors. Capillary Permeability, Alfred Benzon Symposium II. Munksgaard; Copenhagen: 1970. pp. 60–80.
-
- Goresky CA, Ziegler WH, Bach GG. Capillary exchange modeling: Barrier-limited and flow-limited distribution. Circ Res. 1970;27:739–764. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

