Mathematical linearity of circulatory transport
- PMID: 5337940
- PMCID: PMC3024858
- DOI: 10.1152/jappl.1967.22.5.879
Mathematical linearity of circulatory transport
Abstract
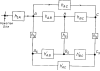
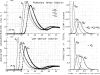
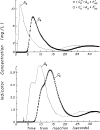
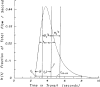
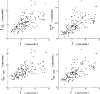
After injections of indocyanine green into the pulmonary artery or left ventricle of anesthetized dogs, indicator-dilution curves were recorded, via identical short sampling systems, from the root of the aorta, the lower thoracic aorta, and the bifurcation of the aorta. The distributions of transit times (transport functions) between each of the three pairs of sampling sites were determined in terms of a mathematical model using the whole of each recorded curve. The accuracy of each transport function was demonstrated by convoluting it with the upstream dilution curve to produce a theoretical downstream dilution curve closely matching the recorded downstream dilution curve. Linearity and stationarity of the aortic system were then tested by comparing the convolution of the transport functions of the upper and lower segments of the aorta with the transport function from aortic root to bifurcation. The results indicate that it is reasonable to apply the superposition principle, as is assumed when calculating flows or mean transit times by indicator-dilution methods, and that cardiac fluctuations in flow produce relatively little error.
Figures
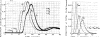
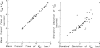
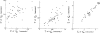
References
-
- Bassingthwaighte JB, Anderson D, Knopp TJ. Effects of unsteady flow on indicator dilution in the circulation. Proc. Ann. Conf. Engnr. Med. Biol., 8th. 1966:184.
-
- Bassingthwaighte JB, Edwards AWT, Wood EH. Areas of dye-dilution curves sampled simultaneously from central and peripheral sites. J. Appl. Physiol. 1962;17:91–98. - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
