Polyoma virus capsid structure at 22.5 A resolution

Abstract

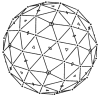
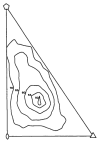
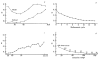
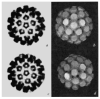
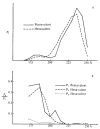
X-ray diffraction data from polyoma capsid crystals were phased by refinement of low-resolution starting models to obtain a self-consistent structural solution. The unexpected result that the hexavalent morphological unit is a pentamer shows that specificity of bonding is not conserved among the protein subunits in the icosahedrally symmetric capsid.

Fig. 1

T = 7d icosahedral surface lattice with five-, three- and two-fold axes marked. The drawing shows one side of the polyhedral surface consisting of 60 six-coordinated and 12 five-coordinated lattice points at the same radius. The location of the six-coordinated point is that determined for the hexavalent morphological unit in the polyoma capsid.

Fig. 2

Location of the hexavalent unit in the icosahedral surface lattice. The R factor comparing the calculated and measured diffraction pattern is plotted as a function of the position of the hexavalent unit in the icosahedral cell defined by the five-, three-and two-fold axes (see Fig. 1). The model giving the smallest R factor is shown in Fig. 3a.

Fig. 3

Density maps of the top half of particles (diameter 495 Å) projected down a two-fold axis (orientation as in Fig. 1). The maps were scaled to have the same total electron density and were photographed directly from a 256 grey scale TV graphics display. a, Model map at 30 Å resolution; b, map computed using observed data and model phases to 30 Å resolution without refinement; c, 30 Å resolution refined map; d, refined map at 22.5 Å resolution calculated by phase extension from 30 Å. Note how the substructure in the morphological units develops as the refinement proceeds. Even at 30 Å resolution the hexavalent unit has a pentagonal appearance.

Fig. 4

R factors comparing the agreement between observed and calculated structure factor amplitudes, a, As a function of resolution comparing initial model and refined map at 30 Å resolution; b, as a function of refinement cycle at 30 Å resolution; c, as a function of resolution for the phase extension from 30 to 22.5 Å resolution; d, as a function of intensity for the 22.5 Å refined map. For a and c the points are plotted so that the interval between points corresponds to equal volume increments in reciprocal space. The starting model (Fig. 3a) fits the observed data best in the 40–50 Å resolution range where there is a strong modulation in the transform determined by the surface lattice arrangement of the morphological units. After 14 cycles of refinement (b) there is a substantial improvement in the fit between the calculated and observed amplitudes at low resolution (a). The structure amplitudes phased by extension from 30 to 22.5 Å resolution represent over half of the total data to this resolution. The R factors for these higher resolution data (c) are uniformly satisfactory. The phase extension also leads to an improvement in the R factor for the data to 30 Å resolution by reducing series termination effects. Plotting the R factor of the 1,343 non-zero reflections as a function of intensity (d) shows that there is a correlation between the R factors and the accuracy of the data which are more precise for the stronger reflections.

Fig. 5

Views of half the capsid (495 Å diameter) down the five-fold axis (a, b) and down the axis of the hexavalent unit (c, d). a And c are computer graphics projections of the electron density map at 22.5 Å resolution, b and c are photographs of a model of stacked sections of the map at 30 Å resolution with the external contour level set at 0.2 of the maximum density. The half-model was built symmetric about the five-fold axis (b), thus, when it is tilted to view down the hexavalent unit (d) the bottom portion of the image is incomplete.

Fig. 6

Rotational power spectra of the pentavalent and hexavalent units. a, P_t is the sum of all cylindrical harmonics in sections of the map through the capsomeres normal to the five-fold axis and the ‘best’ axis of the hexavalent units, plotted as a function of the distance of the section from the centre of the particle. b, Relative strength of the five-fold harmonic of the pentavalent unit and the five- and six-fold harmonic of the hexavalent unit. P_t is proportional to the integrated density in each section. At small radii in the capsid a cylindrical boundary of 93 Å diameter was chosen for calculating the power spectrum of the capsomeres. These cylinders touch at a radius of 170 Å. The integrated density of the inner portions of the capsomere may be underestimated by the methods of calculation. The correspondence in the rotational power spectra distribution of the pentavalent and hexavalent units indicates a close similarity in their structures and a small difference in their radial positions. The relative strength of the order 5 harmonic for the outer portion of both the pentavalent and hexavalent capsomere is reduced because the cylindrically symmetric component, which is the dominant term in P_t, is very strong for this part of the structure. The order 5 harmonic for the hexavalent capsomere is always much stronger than that of order 6 (or any other non-zero harmonic).

Fig. 7

Sections of the electron density map showing substructure of the capsomeres (a–d) and drawings on a polyhedral surface (e, f) illustrating an inferred packing relation of structure units. Upper row: views down five-fold axis and lower row: views down axis of hexavalent capsomere. Width of sections displayed 215 Å. Orientation as in Fig. 5. Grey scales at the bottom show the relation between darkness in the images and map density that increases uniformly from left to right of the scales. a, b, Maps of section planes 215 Å above centre of capsid. At this level and above there is little detectable contact between neighbouring capsomeres. c, d, Maps (displayed with enhanced contrast) of section planes 195 Å above centre. At this level and below five basal parts of the capsomeres splay out and contact basal parts of neighbouring capsomeres. Section planes are perpendicular to the axis of the central capsomere and slice through the neighbouring capsomeres obliquely. In the obliquely sectioned parts the substructure is obscured. Intersections of adjacent planes equidistant from the centre of the capsid that are normal to the axes of the pentavalent and hexavalent capsomeres define 12 equal regular pentagons and 60 equal irregular hexagons. The polygons delineating the domain of the central capsomeres are marked by dotted lines on the density maps. The drawings e and f (constructed on the polyhedral surface made up of the pentagonal and hexagonal facets) illustrate that bonding specificity among identical structure units (represented by graphically cloned mice) cannot be conserved in all the contacts between capsomeres. Arranging structure units in the hexavalent pentamer (centre of f) with quasi-five-fold symmetry resembling the pentagonally symmetric pentamer (centre of e) leads to three types of contacts between structure units of neighbouring pentamers: (1) the two structure units at the top of the central pentamer in f each contact two neighbours (one from the pentavalent and one from another hexavalent pentamer) related by a quasi-three-fold axis; (2) the two structure units below and right of centre in f make quasi-two-fold contacts with neighbours related by an icosahedral three-fold axis; (3) the one structure unit left of centre in f makes an intimate dimer contact with a unit equivalently related by an icosahedral two-fold axis. Thus, the six structure units in the icosahedral asymmetric unit can be put into three categories according to their bonding relations: three in the quasi-trimer, two in the quasi-dimer and one in half the strict dimer.