Efficient coding of natural scenes in the lateral geniculate nucleus: experimental test of a computational theory
- PMID: 8627371
- PMCID: PMC6579125
- DOI: 10.1523/JNEUROSCI.16-10-03351.1996
Efficient coding of natural scenes in the lateral geniculate nucleus: experimental test of a computational theory
Abstract
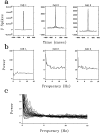
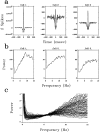
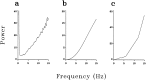
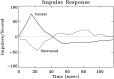
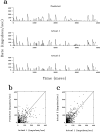
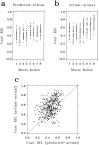
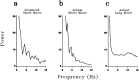
A recent computational theory suggests that visual processing in the retina and the lateral geniculate nucleus (LGN) serves to recode information into an efficient form (Atick and Redlich, 1990). Information theoretic analysis showed that the representation of visual information at the level of the photoreceptors is inefficient, primarily attributable to a high degree of spatial and temporal correlation in natural scenes. It was predicted, therefore, that the retina and the LGN should recode this signal into a decorrelated form or, equivalently, into a signal with a "white" spatial and temporal power spectrum. In the present study, we tested directly the prediction that visual processing at the level of the LGN temporarily whitens the natural visual input. We recorded the responses of individual neurons in the LGN of the cat to natural, time-varying images (movies) and, as a control, to white-noise stimuli. Although there is substantial temporal correlation in natural inputs (Dong and Atick, 1995b), we found that the power spectra of LGN responses were essentially white. Between 3 and 15 Hz, the power of the responses had an average variation of only +/-10.3%. Thus, the signals that the LGN relays to visual cortex are temporarily decorrelated. Furthermore, the responses of X-cells to natural inputs can be well predicted from their responses to white-noise inputs. We therefore conclude that whitening of natural inputs can be explained largely by the linear filtering properties (Enroth-Cugell and Robson, 1966). Our results suggest that the early visual pathway is well adapted for efficient coding of information in the natural visual environment, in agreement with the prediction of the computational theory.
Figures


References
-
- Atick JJ (1992) Could information theory provide an ecological theory of sensory processing? Network: Comput Neural Sys 3:213–251. - PubMed
-
- Atick JJ, Redlich AN. Towards a theory of early visual processing. Neural Comput. 1990;2:308–320.
-
- Atick JJ, Redlich AN. What does the retina know about natural scenes? Neural Comput. 1992;4:196–210.
-
- Atick JJ, Li Z, Redlich AN. Understanding retinal color coding from first principles. Neural Comput. 1992;4:559–572.
-
- Barlow HB. Possible principles underlying the transformation of sensory messages. In: Rosenblith WA, editor. Sensory communication. MIT; Cambridge: 1961.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
