Modeling blood flow heterogeneity
- PMID: 8734057
- PMCID: PMC3212991
- DOI: 10.1007/BF02660885
Modeling blood flow heterogeneity
Abstract
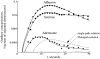
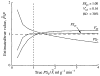
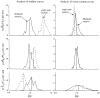
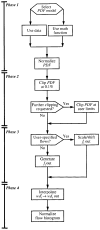
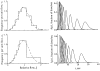
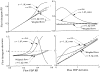
It has been known for some time that regional blood flows within an organ are not uniform. Useful measures of heterogeneity of regional blood flows are the standard deviation and coefficient of variation or relative dispersion of the probability density function (PDF) of regional flows obtained from the regional concentrations of tracers that are deposited in proportion to blood flow. When a mathematical model is used to analyze dilution curves after tracer solute administration, for many solutes it is important to account for flow heterogeneity and the wide range of transit times through multiple pathways in parallel. Failure to do so leads to bias in the estimates of volumes of distribution and membrane conductances. Since in practice the number of paths used should be relatively small, the analysis is sensitive to the choice of the individual elements used to approximate the distribution of flows or transit times. Presented here is a method for modeling heterogeneous flow through an organ using a scheme that covers both the high flow and long transit time extremes of the flow distribution. With this method, numerical experiments are performed to determine the errors made in estimating parameters when flow heterogeneity is ignored, in both the absence and presence of noise. The magnitude of the errors in the estimates depends upon the system parameters, the amount of flow heterogeneity present, and whether the shape of the input function is known. In some cases, some parameters may be estimated to within 10% when heterogeneity is ignored (homogeneous model), but errors of 15-20% may result, even when the level of heterogeneity is modest. In repeated trials in the presence of 5% noise, the mean of the estimates was always closer to the true value with the heterogeneous model than when heterogeneity was ignored, but the distributions of the estimates from the homogeneous and heterogeneous models overlapped for some parameters when outflow dilution curves were analyzed. The separation between the distributions was further reduced when tissue content curves were analyzed. It is concluded that multipath models accounting for flow heterogeneity are a vehicle for assessing the effects of flow heterogeneity under the conditions applicable to specific laboratory protocols, that efforts should be made to assess the actual level of flow heterogeneity in the organ being studied, and that the errors in parameter estimates are generally smaller when the input function is known rather than estimated by deconvolution.
Figures

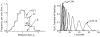
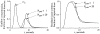



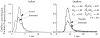
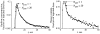




Similar articles
-
Modeling regional myocardial flows from residue functions of an intravascular indicator.Am J Physiol. 1996 Oct;271(4 Pt 2):H1643-55. doi: 10.1152/ajpheart.1996.271.4.H1643. Am J Physiol. 1996. PMID: 8897962 Free PMC article.
-
Modeling the effect of flow heterogeneity on coronary permeability-surface area.J Appl Physiol (1985). 1991 Aug;71(2):758-69. doi: 10.1152/jappl.1991.71.2.758. J Appl Physiol (1985). 1991. PMID: 1938750
-
Estimation of myocardial blood flow heterogeneity by transorgan helium transport functions.Pflugers Arch. 1984 Jul;401(3):217-22. doi: 10.1007/BF00582586. Pflugers Arch. 1984. PMID: 6382151
-
Estimation of blood flow with radioactive tracers.Semin Nucl Med. 1976 Apr;6(2):141-61. doi: 10.1016/s0001-2998(76)80002-5. Semin Nucl Med. 1976. PMID: 775641 Free PMC article. Review.
-
Improving Methods for Discrete Choice Experiments to Measure Patient Preferences [Internet].Washington (DC): Patient-Centered Outcomes Research Institute (PCORI); 2021 Mar. Washington (DC): Patient-Centered Outcomes Research Institute (PCORI); 2021 Mar. PMID: 38386769 Free Books & Documents. Review.
Cited by
-
Network-driven anomalous transport is a fundamental component of brain microvascular dysfunction.Nat Commun. 2021 Dec 15;12(1):7295. doi: 10.1038/s41467-021-27534-8. Nat Commun. 2021. PMID: 34911962 Free PMC article.
-
The mechanical and metabolic basis of myocardial blood flow heterogeneity.Basic Res Cardiol. 2001 Nov;96(6):582-94. doi: 10.1007/s003950170010. Basic Res Cardiol. 2001. PMID: 11770077 Free PMC article. Review.
-
The roles of cerebral blood flow, capillary transit time heterogeneity, and oxygen tension in brain oxygenation and metabolism.J Cereb Blood Flow Metab. 2012 Feb;32(2):264-77. doi: 10.1038/jcbfm.2011.153. Epub 2011 Nov 2. J Cereb Blood Flow Metab. 2012. PMID: 22044867 Free PMC article.
-
Multiscale modeling of cardiac cellular energetics.Ann N Y Acad Sci. 2005 Jun;1047:395-424. doi: 10.1196/annals.1341.035. Ann N Y Acad Sci. 2005. PMID: 16093514 Free PMC article. Review.
-
An integrative model of coupled water and solute exchange in the heart.Am J Physiol Heart Circ Physiol. 2003 Sep;285(3):H1303-16. doi: 10.1152/ajpheart.00933.2001. Epub 2002 Aug 8. Am J Physiol Heart Circ Physiol. 2003. PMID: 12388252 Free PMC article.
References
-
- Abounader R, Vogel J, Kuschinsky W. Patterns of capillary plasma perfusion in brains of conscious rats during normocapnia and hypercapnia. Circ Res. 1995;76:120–126. - PubMed
-
- Audi SH, Krenz GS, Linehan JH, Rickaby DA, Dawson CA. Pulmonary capillary transport function from flow-limited indicators. J Appl Physiol. 1994;77:332–351. - PubMed
-
- Audi SH, Linehan JH, Krenz GS, Dawson CA, Ahlf SB, Roerig DL. Estimation of the pulmonary capillary transport function in isolated rabbit lungs. J Appl Physiol. 1995;78:1004–1014. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
