Bootstrap confidence levels for phylogenetic trees
- PMID: 8917608
- PMCID: PMC24110
- DOI: 10.1073/pnas.93.23.13429
Bootstrap confidence levels for phylogenetic trees
Abstract
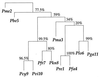
Evolutionary trees are often estimated from DNA or RNA sequence data. How much confidence should we have in the estimated trees? In 1985, Felsenstein [Felsenstein, J. (1985) Evolution 39, 783-791] suggested the use of the bootstrap to answer this question. Felsenstein's method, which in concept is a straightforward application of the bootstrap, is widely used, but has been criticized as biased in the genetics literature. This paper concerns the use of the bootstrap in the tree problem. We show that Felsenstein's method is not biased, but that it can be corrected to better agree with standard ideas of confidence levels and hypothesis testing. These corrections can be made by using the more elaborate bootstrap method presented here, at the expense of considerably more computation.
Figures


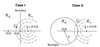
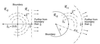
Corrected and republished from
-
Bootstrap confidence levels for phylogenetic trees.Proc Natl Acad Sci U S A. 1996 Jul 9;93(14):7085-90. doi: 10.1073/pnas.93.14.7085. Proc Natl Acad Sci U S A. 1996. Corrected and republished in: Proc Natl Acad Sci U S A. 1996 Nov 12;93(23):13429-34. doi: 10.1073/pnas.93.23.13429. PMID: 8692949 Free PMC article. Corrected and republished.
References
-
- Efron B, Tibshirani R. An Introduction to the Bootstrap. London: Chapman & Hall; 1993.
-
- Felsenstein J. Evolution. 1985;39:783–791. - PubMed
-
- Hillis D, Bull J. Syst Biol. 1993;42:182–192.
-
- Felsenstein J, Kishino H. Syst Biol. 1993;42:193–200.
-
- Newton M A. Biometrika. 1996;83:315–328.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

