New perspectives on forbidden symmetries, quasicrystals, and Penrose tilings
- PMID: 8962037
- PMCID: PMC34472
- DOI: 10.1073/pnas.93.25.14267
New perspectives on forbidden symmetries, quasicrystals, and Penrose tilings
Abstract
Quasicrystals are solids with quasiperiodic atomic structures and symmetries forbidden to ordinary periodic crystals-e.g., 5-fold symmetry axes. A powerful model for understanding their structure and properties has been the two-dimensional Penrose tiling. Recently discovered properties of Penrose tilings suggest a simple picture of the structure of quasicrystals and shed new light on why they form. The results show that quasicrystals can be constructed from a single repeating cluster of atoms and that the rigid matching rules of Penrose tilings can be replaced by more physically plausible cluster energetics. The new concepts make the conditions for forming quasicrystals appear to be closely related to the conditions for forming periodic crystals.
Figures

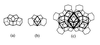
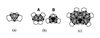
References
-
- Penrose R. Bull Inst Math Appl. 1974;10:266–269.
-
- Levine D, Steinhardt P J. Phys Rev Lett. 1984;53:2477–2480.
-
- Levine D, Steinhardt P J. Phys Rev B Solid State. 1986;34:596–616. - PubMed
-
- Steinhardt P J. Am Sci. 1986;74:586–597.
-
- Steinhardt P J, Jeong H-C. Nature (London) 1996;382:433–435.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

