Linearized buffered Ca2+ diffusion in microdomains and its implications for calculation of [Ca2+] at the mouth of a calcium channel
- PMID: 9278532
- PMCID: PMC6573285
- DOI: 10.1523/JNEUROSCI.17-18-06961.1997
Linearized buffered Ca2+ diffusion in microdomains and its implications for calculation of [Ca2+] at the mouth of a calcium channel
Abstract
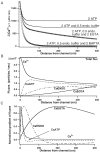
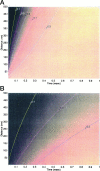
Immobile and mobile calcium buffers shape the calcium signal close to a channel by reducing and localizing the transient calcium increase to physiological compartments. In this paper, we focus on the impact of mobile buffers in shaping steady-state calcium gradients in the vicinity of an open channel, i.e. within its "calcium microdomain." We present a linear approximation of the combined reaction-diffusion problem, which can be solved explicitly and accounts for an arbitrary number of calcium buffers, either endogenous or added exogenously. It is valid for small saturation levels of the present buffers and shows that within a few hundred nanometers from the channel, standing calcium gradients develop in hundreds of microseconds after channel opening. It is shown that every buffer can be assigned a uniquely defined length-constant as a measure of its capability to buffer calcium close to the channel. The length-constant clarifies intuitively the significance of buffer binding and unbinding kinetics for understanding local calcium signals. Hence, we examine the parameters shaping these steady-state gradients. The model can be used to check the expected influence of single channel calcium microdomains on physiological processes such as excitation-secretion coupling or excitation-contraction coupling and to explore the differential effect of kinetic buffer parameters on the shape of these microdomains.
Figures

Similar articles
-
On calcium-buffer dynamics within the excess buffer regime.J Theor Biol. 2010 May 7;264(1):55-65. doi: 10.1016/j.jtbi.2010.01.017. Epub 2010 Jan 20. J Theor Biol. 2010. PMID: 20093125
-
The local Ca concentration profile in the vicinity of a Ca channel.Cell Biochem Biophys. 2001;35(1):49-61. doi: 10.1385/CBB:35:1:49. Cell Biochem Biophys. 2001. PMID: 11898855
-
Modeling study of the effects of overlapping Ca2+ microdomains on neurotransmitter release.Biophys J. 1999 Feb;76(2):735-50. doi: 10.1016/S0006-3495(99)77240-1. Biophys J. 1999. PMID: 9929478 Free PMC article.
-
Presynaptic Ca2+ dynamics, Ca2+ buffers and synaptic efficacy.Cell Calcium. 2005 May;37(5):489-95. doi: 10.1016/j.ceca.2005.01.003. Cell Calcium. 2005. PMID: 15820398 Review.
-
Buffer mobility and the regulation of neuronal calcium domains.Front Cell Neurosci. 2015 Feb 20;9:48. doi: 10.3389/fncel.2015.00048. eCollection 2015. Front Cell Neurosci. 2015. PMID: 25750615 Free PMC article. Review.
Cited by
-
Complexin stabilizes newly primed synaptic vesicles and prevents their premature fusion at the mouse calyx of held synapse.J Neurosci. 2015 May 27;35(21):8272-90. doi: 10.1523/JNEUROSCI.4841-14.2015. J Neurosci. 2015. PMID: 26019341 Free PMC article.
-
Electrical tuning and transduction in short hair cells of the chicken auditory papilla.J Neurophysiol. 2013 Apr;109(8):2007-20. doi: 10.1152/jn.01028.2012. Epub 2013 Jan 30. J Neurophysiol. 2013. PMID: 23365177 Free PMC article.
-
Bound Ca2+ moves faster and farther from single open channels than free Ca2.Front Physiol. 2023 Dec 20;14:1266120. doi: 10.3389/fphys.2023.1266120. eCollection 2023. Front Physiol. 2023. PMID: 38173931 Free PMC article.
-
Relating a calcium indicator signal to the unperturbed calcium concentration time-course.Theor Biol Med Model. 2007 Feb 6;4:7. doi: 10.1186/1742-4682-4-7. Theor Biol Med Model. 2007. PMID: 17284310 Free PMC article.
-
Modulation of Dopaminergic Neuronal Excitability by Zinc through the Regulation of Calcium-related Channels.Exp Neurobiol. 2019 Oct 31;28(5):578-592. doi: 10.5607/en.2019.28.5.578. Exp Neurobiol. 2019. PMID: 31698550 Free PMC article.
References
-
- Allbritton NL, Meyer T, Stryer L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 1992;258:1812–1815. - PubMed
-
- Augustine GJ, Adler EM, Charlton MP. The calcium signal for transmitter secretion from presynaptic nerve terminals. Ann NY Acad Sci. 1991;635:365–381. - PubMed
-
- Augustine GJ, Neher E. Neuronal Ca2+ signaling takes the local route. Curr Opin Neurobiol. 1992b;2:302–307. - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Miscellaneous
