The kinetics of L-selectin tethers and the mechanics of selectin-mediated rolling
- PMID: 9281593
- PMCID: PMC2136756
- DOI: 10.1083/jcb.138.5.1169
The kinetics of L-selectin tethers and the mechanics of selectin-mediated rolling
Abstract
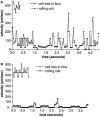
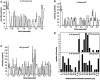
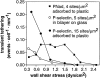
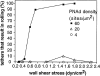
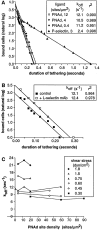
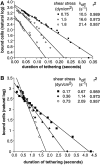
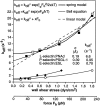
Two mechanisms have been proposed for regulating rolling velocities on selectins. These are (a) the intrinsic kinetics of bond dissociation, and (b) the reactive compliance, i.e., the susceptibility of the bond dissociation reaction to applied force. To determine which of these mechanisms explains the 7.5-11.5-fold faster rolling of leukocytes on L-selectin than on E- and P-selectins, we have compared the three selectins by examining the dissociation of transient tethers. We find that the intrinsic kinetics for tether bond dissociation are 7-10-fold more rapid for L-selectin than for E- and P-selectins, and are proportional to the rolling velocities through these selectins. The durations of pauses during rolling correspond to the duration of transient tethers on low density substrates. Moreover, applied force increases dissociation kinetics less for L-selectin than for E- and P-selectins, demonstrating that reactive compliance is not responsible for the faster rolling through L-selectin. Further measurements provide a biochemical and biophysical framework for understanding the molecular basis of rolling. Displacements of tethered cells during flow reversal, and measurements of the distance between successive pauses during rolling provide estimates of the length of a tether and the length of the adhesive contact zone, and suggest that rolling occurs with as few as two tethers per contact zone. Tether bond lifetime is an exponential function of the force on the bond, and the upper limit for the tether bond spring constant is of the same order of magnitude as the estimated elastic spring constant of the lectin-EGF unit. Shear uniquely enhances the rate of L-selectin transient tether formation, and conversion of tethers to rolling adhesions, providing further understanding of the shear threshold requirement for rolling through L-selectin.
Figures
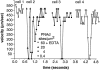
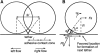
References
-
- Alon R, Hammer DA, Springer TA. Lifetime of the P-selectin; carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature (Lond) 1995;374:539. - PubMed
-
- Bargatze RF, Jutila MA, Butcher EC. Distinct roles of L-selectin and integrins α4β7 and LFA-1 in lymphocyte homing to Peyer's patch-HEV in situ: the multistep model confirmed and refined. Immunity. 1995;3:99–108. - PubMed
-
- Bell GI. Models for the specific adhesion of cells to cells: a theoretical framework for adhesion mediated by reversible bonds between cell surface molecules. Science (Wash DC) 1978;200:618–627. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

