Linearity and normalization in simple cells of the macaque primary visual cortex
- PMID: 9334433
- PMCID: PMC6573724
- DOI: 10.1523/JNEUROSCI.17-21-08621.1997
Linearity and normalization in simple cells of the macaque primary visual cortex
Abstract
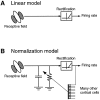
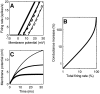
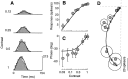
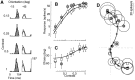
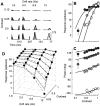
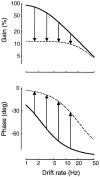
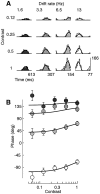
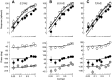
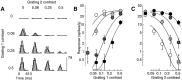
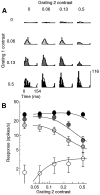
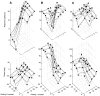
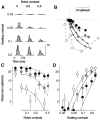
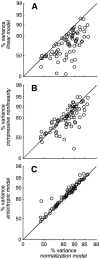
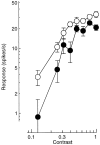
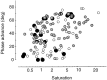
Simple cells in the primary visual cortex often appear to compute a weighted sum of the light intensity distribution of the visual stimuli that fall on their receptive fields. A linear model of these cells has the advantage of simplicity and captures a number of basic aspects of cell function. It, however, fails to account for important response nonlinearities, such as the decrease in response gain and latency observed at high contrasts and the effects of masking by stimuli that fail to elicit responses when presented alone. To account for these nonlinearities we have proposed a normalization model, which extends the linear model to include mutual shunting inhibition among a large number of cortical cells. Shunting inhibition is divisive, and its effect in the model is to normalize the linear responses by a measure of stimulus energy. To test this model we performed extracellular recordings of simple cells in the primary visual cortex of anesthetized macaques. We presented large stimulus sets consisting of (1) drifting gratings of various orientations and spatiotemporal frequencies; (2) plaids composed of two drifting gratings; and (3) gratings masked by full-screen spatiotemporal white noise. We derived expressions for the model predictions and fitted them to the physiological data. Our results support the normalization model, which accounts for both the linear and the nonlinear properties of the cells. An alternative model, in which the linear responses are subject to a compressive nonlinearity, did not perform nearly as well.
Figures

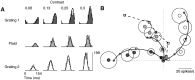

References
-
- Adelson EH, Bergen JR. Spatiotemporal energy models for the perception of motion. J Opt Soc Am A. 1985;2:284–299. - PubMed
-
- Albrecht DG. Visual cortex neurons in monkey and cat: effect of contrast on the spatial and temporal phase transfer functions. Vis Neurosci. 1995;12:1191–1210. - PubMed
-
- Albrecht DG, Geisler WS. Motion sensitivity and the contrast-response function of simple cells in the visual cortex. Vis Neurosci. 1991;7:531–546. - PubMed
-
- Albrecht DG, Hamilton DB. Striate cortex of monkey and cat: contrast response function. J Neurophysiol. 1982;48:217–237. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
