Kinetics of recovery of the dark-adapted salamander rod photoresponse
- PMID: 9417132
- PMCID: PMC1887775
- DOI: 10.1085/jgp.111.1.7
Kinetics of recovery of the dark-adapted salamander rod photoresponse
Abstract
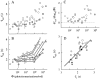
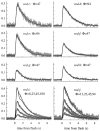
The kinetics of the dark-adapted salamander rod photocurrent response to flashes producing from 10 to 10(5) photoisomerizations (Phi) were investigated in normal Ringer's solution, and in a choline solution that clamps calcium near its resting level. For saturating intensities ranging from approximately 10(2) to 10(4) Phi, the recovery phases of the responses in choline were nearly invariant in form. Responses in Ringer's were similarly invariant for saturating intensities from approximately 10(3) to 10(4) Phi. In both solutions, recoveries to flashes in these intensity ranges translated on the time axis a constant amount (tauc) per e-fold increment in flash intensity, and exhibited exponentially decaying "tail phases" with time constant tauc. The difference in recovery half-times for responses in choline and Ringer's to the same saturating flash was 5-7 s. Above approximately 10(4) Phi, recoveries in both solutions were systematically slower, and translation invariance broke down. Theoretical analysis of the translation-invariant responses established that tauc must represent the time constant of inactivation of the disc-associated cascade intermediate (R*, G*, or PDE*) having the longest lifetime, and that the cGMP hydrolysis and cGMP-channel activation reactions are such as to conserve this time constant. Theoretical analysis also demonstrated that the 5-7-s shift in recovery half-times between responses in Ringer's and in choline is largely (4-6 s) accounted for by the calcium-dependent activation of guanylyl cyclase, with the residual (1-2 s) likely caused by an effect of calcium on an intermediate with a nondominant time constant. Analytical expressions for the dim-flash response in calcium clamp and Ringer's are derived, and it is shown that the difference in the responses under the two conditions can be accounted for quantitatively by cyclase activation. Application of these expressions yields an estimate of the calcium buffering capacity of the rod at rest of approximately 20, much lower than previous estimates.
Figures



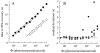







Similar articles
-
The role of steady phosphodiesterase activity in the kinetics and sensitivity of the light-adapted salamander rod photoresponse.J Gen Physiol. 2000 Dec;116(6):795-824. doi: 10.1085/jgp.116.6.795. J Gen Physiol. 2000. PMID: 11099349 Free PMC article.
-
The kinetics of inactivation of the rod phototransduction cascade with constant Ca2+i.J Gen Physiol. 1996 Jan;107(1):19-34. doi: 10.1085/jgp.107.1.19. J Gen Physiol. 1996. PMID: 8741728 Free PMC article.
-
Analysis of Ca++-dependent gain changes in PDE activation in vertebrate rod phototransduction.Mol Vis. 2000 Dec 31;6:265-86. Mol Vis. 2000. PMID: 11139649 Free PMC article.
-
Tuning outer segment Ca2+ homeostasis to phototransduction in rods and cones.Adv Exp Med Biol. 2002;514:179-203. doi: 10.1007/978-1-4615-0121-3_11. Adv Exp Med Biol. 2002. PMID: 12596922 Review.
-
Electrical and adaptive properties of rod photoreceptors in Bufo marinus. I. Effects of altered extracellular Ca2+ levels.J Gen Physiol. 1977 Dec;70(6):747-70. doi: 10.1085/jgp.70.6.747. J Gen Physiol. 1977. PMID: 412914 Free PMC article. Review.
Cited by
-
Cones respond to light in the absence of transducin β subunit.J Neurosci. 2013 Mar 20;33(12):5182-94. doi: 10.1523/JNEUROSCI.5204-12.2013. J Neurosci. 2013. PMID: 23516284 Free PMC article.
-
Speed, sensitivity, and stability of the light response in rod and cone photoreceptors: facts and models.Prog Retin Eye Res. 2012 Sep;31(5):442-66. doi: 10.1016/j.preteyeres.2012.05.002. Epub 2012 May 29. Prog Retin Eye Res. 2012. PMID: 22658984 Free PMC article. Review.
-
Engineering aspects of enzymatic signal transduction: photoreceptors in the retina.Biophys J. 2000 Dec;79(6):2801-17. doi: 10.1016/S0006-3495(00)76519-2. Biophys J. 2000. PMID: 11106590 Free PMC article.
-
Kinetics of turn-offs of frog rod phototransduction cascade.J Gen Physiol. 2008 Nov;132(5):587-604. doi: 10.1085/jgp.200810034. J Gen Physiol. 2008. PMID: 18955597 Free PMC article.
-
The calculus of rod phototransduction.J Gen Physiol. 1998 Jan;111(1):3-6. doi: 10.1085/jgp.111.1.3. J Gen Physiol. 1998. PMID: 9417131 Free PMC article. Review. No abstract available.
References
-
- Aczel, J. 1966. Lectures on functional equations and their applications. Academic Press, New York.
-
- Adelson EH. The delayed rod afterimage. Vision Res. 1982a;22:1313–1328. - PubMed
-
- Adelson EH. Saturation and adaptation in the rod system. Vision Res. 1982b;22:1299–1312. - PubMed
-
- Angleson JK, Wensel TG. Enhancement of rod outer segment GTPase accelerating protein activity by the inhibitory subunit of GMP phosphodiesterase. J Biol Chem. 1994;269:16290–16296. - PubMed
-
- Arshavsky VY, Gray-Keller MP, Bownds MD. cGMP suppresses GTPase activity of portion of transducin equimolar to phosphodiesterase in frog rod outer segments. Light-induced cGMP decreases as a putative feedback mechanism of the photoresponse. J Biol Chem. 1991;266:18530–18537. - PubMed

