Activation of Shaker potassium channels. III. An activation gating model for wild-type and V2 mutant channels

Abstract

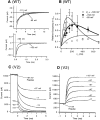
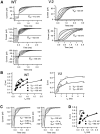
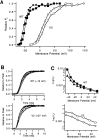
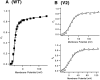
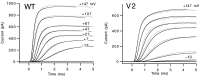
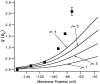
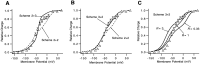
A functional kinetic model is developed to describe the activation gating process of the Shaker potassium channel. The modeling in this paper is constrained by measurements described in the preceding two papers, including macroscopic ionic and gating currents and single channel ionic currents. These data were obtained from the normally activating wild-type channel as well as a mutant channel V2, in which the leucine at position 382 has been mutated to a valine. Different classes of models that incorporate Shaker's symmetrical tetrameric structure are systematically examined. Many simple gating models are clearly inadequate, but a model that can account for all of the qualitative features of the data has the channel open after its four subunits undergo three transitions in sequence, and two final transitions that reflect the concerted action of the four subunits. In this model, which we call Scheme 3+2', the channel can also close to several states that are not part of the activation path. Channel opening involves a large total charge movement (10.8 e0), which is distributed among a large number of small steps each with rather small charge movements (between 0.6 and 1.05 e0). The final two transitions are different from earlier steps by having slow backward rates. These steps confer a cooperative mechanism of channel opening at Shaker's activation voltages. In the context of Scheme 3+2', significant effects of the V2 mutation are limited to the backward rates of the final two transitions, implying that L382 plays an important role in the conformational stability of the final two states.

Figure 7

Fits of Scheme 2+2′ to WT and V2's ionic and gating current time courses at depolarized test voltages up to +147 mV. (A) A comparison of the measured and simulated ionic current time courses indicate that Scheme 2+2′ accounts for the channel opening kinetics quite well; the deviation at very large test depolarizations (especially prominent for V2) reflect the contribution of channel openings through a slow alternate activation path (C_i states; Schoppa and Sigworth, 1998a ) that is not included in the model. The holding potential was −93 mV. Data are from patches w312 and v096. (B) The measured/simulated currents in A were fitted to yield values for the activation time constant τ_a (squares, bold lines) and delay δ_a (circles, regular lines) using the strategy of Schoppa and Sigworth (1998a). At V ≥ +67 mV, the measured τ_a values reflect the fast time constant obtained in fits of the currents to the sum of two exponentials. (C) Fits of WT's and V2's gating currents at voltages between −13 and +47 mV (solid curves). The requirement for cooperative interaction (c > 1) for S₀ ↔ S₁ is illustrated by the discrepancy in the fits of WT's on gating currents to Scheme 2+2′ for no interaction (c = 1; dashed curves). Data are from patches w212 and v219. The holding potential was −93 mV in these recordings. (D) WT's gating current time course was used to place an upper limit on the degree of cooperative interaction assigned to S₀ ↔ S₁. For interactions corresponding to values of c = 1.5 and 2.0, values for a ₁(0) were first adjusted to best account for WT's ionic current time courses at −13 mV (left). The resulting predictions for the gating currents at −13 mV on the right indicate that c ≥ 1.5 yields a predicted current with a peak that is too broad. To facilitate comparison, the simulated currents for c = 1.5 and 2.0 were scaled to peak at the same value as the current predicted by c = 1.3.

Figure 3

Fits of Scheme 0+2′ to selected WT and V2 macroscopic ionic current time courses that reflect the final transitions. For WT, these include (A) tail currents at voltages between −93 and −193 mV (patch w448), and (B) time-dependent occupancies in the last closed state in the activation path C_N-1, derived from reactivation time courses. Occupancies in C_N-1 are indicated for hyperpolarizations to voltages V _h = −93, −153, and −193 mV as a function of the hyperpolarization duration t _h. Occupancy estimates were derived from the amplitude of the fast reactivation component, as described in a previous paper (Schoppa and Sigworth, 1998a ), and reflect averages from one to four experiments. In the simulations of these data, we set α_N-1 = 0 during the test pulse, or, effectively, β_N-2 >> α_N-1 at V ≤ −93 mV. Scheme 0+2′ also accounts for (C) V2's macroscopic ionic tail currents at voltages between −73 and +27 mV, and (D) V2's channel opening time courses after a prepulse to +7 mV. In D, the prepulse loads most channels into the last closed states, so that the test currents mostly reflect the kinetics of the final two transitions. All V2 data are from the same patch (v329).

Figure 10

Fits of Scheme 2+2′ to WT and V2 reactivation kinetics. (A) Scheme 2+2′ accounts for WT and V2's reactivation time courses after hyperpolarizations of various amplitudes V _h (between −53 and −193 mV) and duration t _h. Test voltages were +37 and +67 mV for WT and V2, respectively. All of the displayed data come from the same WT and V2 patch recordings and correspond to the following t _h values. WT: for V _h = −113 mV, t _h = 0.5, 0.7, 1, and 2 ms; for V _h = −153 mV, t _h = 0.1, 0.2, 0.3, 0.4, 0.5, 0.7, and 1 ms; for V _h = −193 mV, t _h = 0.1, 0.2, 0.3, 0.4, and 0.6 ms. V2: for V _h = −53 mV, t _h = 0.2, 0.5, 1, 2, and 5 ms; for V _h = −53 mV, t _h = 0.1, 0.2, 0.5, 1, and 5 ms. In the simulations, for WT, a ₁ and a ₂ were each increased by 20% compared with the values in Table II, and the values for β_N-1(0) and β_N(0) were 520 and 280 s⁻¹. For V2, β_N was changed to 1,100 s⁻¹. Data are from patches w448 and v162. (B) Scheme 2+2′ accounts for the delay δ_a in WT and V2's reactivation time course for different V _h and t _h. The δ_a values were derived from the measured and simulated currents from A. (C and D) WT's reactivation time courses were used to place constraints on the sizes of q _b1 and q _b2. For reactivation time courses measured after V _h = −193 mV, values for q _b1 and q _b2 that are two or three times as large as the values in Table II predict a reactivation delay that is too long. In D, the three superimposed lines to the left of the squares reflect δ_a values derived from simulated currents for the q _b1 and q _b2 values in Table II (the best fit) or q _b1 and q _b2 values that are two or three times larger. For these simulations, the values of b ₁(0) and b ₂(0) were first adjusted to achieve good fits of WT's reactivation time course for V _h = −113 mV (shown by the derived δ_a values in D).

Figure 1

Patch-to-patch variabilities are apparent in WT and V2 voltage dependence of P _o (A) and ionic current time courses (B). The P _o -V plots were taken from two different patches each for WT and V2, and time courses were taken from seven different patches. The test voltages for the currents in B were −13 and +27 mV for WT and V2, respectively. (C) A comparison of the τ_a values at different test voltages from two WT and V2 patches shows that the variability in the current kinetics is well accounted for by a simple voltage shift.

Figure 11

Scheme 2+2′ accounts for some but not all of the features of WT's and V2's equilibrium voltage dependence of channel opening and charge movement. WT and V2 plots are shown with ordinates that are either linear (A) or log transformed (B). The discrepancies in the fits are the largest for V2's linearly plotted Q-V relation and for WT's log-transformed values of P _o. The model also slightly underestimates the steepness of the Q-V relation at the most hyperpolarized voltages (seen in B). For the linear plot, the values reflect mean ± SEM from one to eight experiments. The log-transformed data reflect single patch experiments (WT patches w158 and w249; V2 patches v206 and v240).

Figure 5

Fits of Scheme 0+2′ to the equilibrium P _o at depolarized voltages for WT (A) and V2 (B). For V2, we have fitted P _o -V relations obtained from current measurements made in two patches (v096 and v142). For WT, we have fitted the mean P _o -V relation, since its complete P _o -V relation was constructed using observations that were made in more than one patch (Schoppa and Sigworth, 1998a ). In fitting WT's P _o -V relation, we are here only interested in the shape of the P _o -V relation at depolarized voltages, but needed to add several early transitions to Scheme 0+2′ to approximate P _o at lower voltages. The model used wasin which we have added one set of four subunit transitions to Scheme 0+2′. For the modified model, the charge associated with S₀ ↔ S₁ was set at 2.55 e₀ and its midpoint voltage was −53 mV. The simulations for V2 reflect Scheme 0+2′, but the values for β_N-1(0) varied slightly from those in Table I; for the two patches, β_N-1(0) was 17,000 and 14,000 s⁻¹.

Figure 16

Scheme 3+2′ accounts for some but not all of WT's and V2's reactivation time courses. (A) Selected WT and V2 reactivation time courses from Fig. 10 were fitted to Scheme 3+2′. Scheme 3+2′ accounts for the reactivation time courses for the less negative V _h reasonably well, but fails to account for the reactivation time courses for the most negative V _h. In these simulations, for WT, the values of a ₁, a ₂, and a ₃ were each increased by 20% compared with the values in Table III, and the values for β_N-1(0) and β_N(0) were 520 s⁻¹ and β_N = 280 s⁻¹. For V2, β_N was changed to 1,100 s⁻¹. (B) The same deviations in the fits are shown in a comparison of the δ_a values that were derived from the measured and simulated currents in A. These discrepancies reflect the 20% increases in q _b1, q _b2, and q _b3, used to help achieve a sufficiently large total gating charge.

Figure 18

Fits of Scheme 3+2′ to WT's and V2's ionic current measured after prepulses of different amplitude V _p. The test voltages used were +37 mV for WT and +107 mV for V2. (A) Scheme 3+2′ accounts well for the current time courses measured for wide range of V _p values. These simulations were made while incorporating changes to Scheme 3+2′ identical to those described for Scheme 2+2′ in Fig. 8; that is, we include the transition from the last closed state to the state C_iN-1 (and also the transition C_iN-1 ↔ C_iN). The rates for these additional transitions are those given in the legend to Fig. 8, except that rate of C_N-1 → C_iN-1 for V2 (at +147 mV) was increased from 6,700 to 8,600 s⁻¹, to account for the relatively large amplitude of the slow activation component observed in this patch recording. Also, for WT, a ₁, a ₂, and a ₃, were each increased by 4% compared with the values in Table III; for V2, each were increased by 10%. Data are from patches w139 and v148. (B and C) The good fits of the ionic currents are also reflected in a comparison of the normalized τ_a and δ_a parameters (symbols, lines) derived from the measured/simulated currents for different V _p. WT's and V2's experimental τ_a and δ_a values reflect the mean ± SEM from one to four experiments. The τ_a values derived from V2's measured/simulated currents reflect the fast time constant in fits of these currents to the sum of two exponentials.

Figure 8

A modified version of Scheme 2+2′ accounts for a slow component in the activation time course. In this model, the channel can enter the state C_iN-1 from the last closed state C_N-1. A transition between C_iN-1 and C_iN is also allowed. The indicated rates of the added transitions are for +147 mV, where the slow component is prominent in the ionic current. The partial charges associated with these transitions were set to be identical to those associated with the parallel transitions; e.g., the charges for C_N-1 ↔ C_iN-1 are the same as for O_N ↔ C_iN. The rates for the other transitions in the model are nearly identical to the rates for Scheme 2+2′, given in Tables I and II. Rates for V2 are boxed. The one exception is that the rate d for WT had to be increased slightly (from 600 to 1,000 s⁻¹) to account for WT's kinetics in this patch; being the slowest “forward” rate in the alternate path (at +147 mV), the rate d sets the time course of the slow component. The amplitude of the slow component is largely set by the rate of C_N-1 → C_iN-1, as well as the occupancy in C_N-1. Interestingly, the model accounts for the fourfold larger amplitude of the slow component for V2 without a substantial change in C_N-1 → C_iN-1, suggesting that the difference in WT's and V2's ionic current arises from differential occupancy in C_N-1. For reference, the values of the other relevant rate constants at +147 mV are (s⁻¹), for WT: α_N-1 = 540,000, β_N-1 = 60, α_N = 19,000, β_N = 12, c = 22, d = 1,000; for V2: α_N-1 = 290,000, β_N-1 = 3,300, α_N = 10,200, β_N = 32, c = 54, d = 600.

Figure 2

Classes of gating models for Shaker potassium channels. For each model, each of four subunits undergoes one, two, or three transitions between subunit states, designated by S₀, S₁, etc. In some of the models, the channel undergoes one, two, or three additional concerted transitions. The models are named by the number of subunit transitions and additional concerted transitions. For models with no concerted transitions, the channel is taken to be open after the fourth subunit has undergone the last subunit transition; this is indicated by the dashed line to the open state.

Figure 4

Fits of Scheme 0+2′ to the single-channel closed and open dwell-time histograms at depolarized voltages for WT (A) and V2 (B). For each channel, the closed time histograms are shown on the left, and open times on the right. Solid curves reflect the predictions of Scheme 0+2′ with the values in Table I. The dashed curves on V2's histograms were computed with parameters that are modified from those in Table I in the following way: β_N-1(0) was set to 4,400 s⁻¹ and the value α_N-1(0) = 300 s⁻¹ was chosen to best fit the closed time histograms. The solid and dashed curves are not always distinguishable. All data are from the same two patches (w265 and v433), except at +107 mV (w266 and v344).

Figure 6

The magnitude of the average, absolute charge movement per channel at negative voltages was used to test the “n ⁴” scheme as a model of the first gating transitions. The solid curves were computed from a model assuming a number p of equivalently acting subunits, for which the charge movement q is given by For each curve the charge z ₁ and midpoint voltage V ₁ for the transition were fixed to 0.89 and −53 mV, which are the charge and midpoint voltage values of the very first gating transition derived from the kinetic estimates of α₁ and β₁. The displayed charge values reflect the same data as in Fig. 1 in Schoppa and Sigworth (1998a), except scaled by the estimate of the single channel charge movement q = 12.3 e₀ reported in Schoppa et al. (1992). The error bars are smaller than the symbols for most of the values.

Figure 9

Scheme 2+2′ accounts for WT's and V2's gating currents at hyperpolarized voltages. Simulations are shown for (A) currents induced by voltage steps between −93 mV and more negative voltages (patches w249 and v240) and (B) currents induced by step hyperpolarizations from intermediate prepulse voltages (patches w217 and v417). In B, the duration of the prepulse was 2 and 20 ms for WT and V2, respectively. A short prepulse was used for WT to minimize the contribution of channels in the open state to the gating current time course.

Figure 12

Constraints on how to add more transitions to Scheme 2+2′ were provided by the shape of V2's Q-V relation. (A) V2's mean Q-V relation has been superimposed (solid curve) with predictions of Scheme 2+3′, with the concerted transition in the third to last position having a valence of 3.5. This model steepens the Q-V relation compared with the predictions of Scheme 2+2′ (dashed curve). However, it yields a Q-V relation that is too steep at voltages near −40 mV, while remaining too shallow at hyperpolarized voltages (near −80 mV). For the simulations, the parameter estimates for all but the large valenced transition were fixed to be the same as in Scheme 2+2′; the midpoint voltage of the new transition was varied to best account for V2's Q-V relation. (B) Scheme 3+2′ performs better at steepening V2's Q-V relation across the entire voltage range. For these simulations, the parameter values for S₀ ↔ S₁ and S₁ ↔ S₂ were those given for the same transitions in Scheme 2+2′ in Table II. For S₂ ↔ S₃, we assigned a charge (0.88 e₀) that is one-fourth of the charge (3.5 e₀) assigned to the concerted transition in Scheme 2+3′ in A. Its midpoint voltage was varied to yield the best fits of the data. (C) V2's Q-V relation was also used to obtain a rough estimate of the equilibrium constant for S₂ ↔ S₃. Three different simulations of Scheme 3+2′ are shown for different values of a factor R (R = 3, 1, and 0.33) that reflect the ratio of the equilibrium of S₂ ↔ S₃ versus that of S₁ ↔ S₂. In these simulations, the charge associated with S₂ ↔ S₃ was assigned to be the same as that associated with S₁ ↔ S₂, given in Table II.

Figure 13

Scheme 3+2′ accounts for WT's and V2's macroscopic ionic current time courses across a wide voltage range. Simulations are shown for currents measured at depolarized voltages (A) and at intermediate voltages (B). The holding potential was −93 mV. To allow comparison of Scheme 3+2′ with Scheme 2+2′, the simulations of activation time courses here were made while incorporating changes to Scheme 3+2′ identical to those made for Scheme 2+2′ in Fig. 8; we have added a transition from the last closed state to the state C_iN-1 (and also the transition C_iN-1 ↔ C_iN). The rates for these additional transitions are those given in the legend to Fig. 8. All current traces for WT and V2 come from the same two WT and V2 patches (w312 and v096). (C) The good fits of the ionic currents are also reflected in a comparison of the τ_a and δ_a parameters (symbols, lines) derived from the measured/simulated currents. The τ_a values at high depolarized voltages (V ≥ +67 mV) reflect the fast time constant in fits of the measured and simulated currents to the sum of two exponentials.

Figure 14

Scheme 3+2′ accounts for WT's and V2's on gating currents across a wide voltage range, between −73 and +47 mV. All current traces come from the same two WT and V2 patches (w212 and v219). Notably, at −33 mV, the model accounts for a slow component that is present in WT's current, but absent in V2's current. The holding potential was −93 mV in these recordings.

Figure 15

Scheme 3+2′ accounts for WT and V2's gating currents at most hyperpolarized voltages. Simulations are shown for (A) currents induced by voltage steps between −93 mV and more negative voltages, and (B) currents induced by step hyperpolarizations from intermediate prepulse voltages. Data are identical to the traces in Fig. 9. For the most negative test voltage in A (−153 mV), Scheme 3+2′ predicts a current that decays too rapidly, by roughly a factor of 2. This discrepancy reflects the 20% increase in q _b1 that was introduced to help achieve a sufficiently large total gating charge (see text).

Figure 17

Scheme 3+2′ performs much better than Scheme 2+2′ at predicting certain features of WT's and V2's equilibrium voltage dependence of channel opening and charge movement, including the steepness of V2's Q-V relation and the voltage sensitivity of WT's P _o at low P _o. As in Fig. 11, plots are shown with ordinates that are linear (A) or log transformed (B).

Figure 19

Fits of Scheme 3+2′ to WT's and V2's off gating currents after a range of prepulses of different amplitude V _p (A) and different duration t _p (B). In B, WT's currents were measured after different prepulses to −33 mV that ranged in duration from 30 to 2 ms (bottom to top). The test voltage for all recordings was −93 mV. For WT's currents, the model accounts for the development of a slowly decaying off current with an increase in the amplitude or duration of the prepulse. The model also accounts for V2's faster off current decay kinetics. The arrow on V2's off current after a prepulse to +27 mV in A marks a small inflection in the simulated current that corresponds to a plateau phase. Data from patches w212 and v219 in A, and patch w217 in B.