Models of ensemble firing of muscle spindle afferents recorded during normal locomotion in cats

Abstract

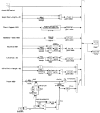
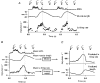
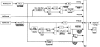
1. The aim of this work was to compare the ability of several mathematical models to predict the firing characteristics of muscle spindle primary afferents recorded chronically during normal stepping in cats. 2. Ensemble firing profiles of nine hamstring spindle primary (presumed group Ia) afferents were compiled from stored data from 132 step cycles. Three sets of profiles corresponding to slow, medium and fast steps were generated by averaging groups of step cycles aligned to peak muscle length in each cycle. 3. Five models obtained from the literature were compared. Each of these models was used to predict the spindle firing profiles from the averaged muscle length signals. The models were also used in the reverse direction, namely to predict muscle length from the firing profiles. A sixth model incorporating some key aspects of the other models was also included in the comparisons. 4. Five of the models predicted spindle firing well, with root mean square (r.m.s.) errors lower than 14 % of the modulation depth of the target profiles. The key variable in achieving good predictions was muscle velocity, the best fits being obtained with power-law functions of velocity, with an exponent of 0.5 or 0.6 (i.e. spindle firing rate is approximately proportional to the square root of muscle velocity). The fits were slightly improved by adding small components of EMG signal to mimic fusimotor action linked to muscle activation. The modest relative size of EMG-linked fusimotor action may be related to the fact that hamstring muscles are not strongly recruited in stepping. 5. Length was predicted very accurately from firing profiles with the inverse of the above models, indicating that the nervous system could in principle process spindle firing in a relatively simple way to give accurate information on muscle length. 6. The responses of the models to standard ramp-and-hold displacements at 10 mm s-1 were also studied (i.e. velocities that were an order of magnitude lower than that during stepping). In these cases components of spindle primary response related to length as well as velocity were needed for good fits. Because these length-related components detracted from rather than improved predictions of the step cycle data, an attenuation of length dependence at high muscle velocities emerged as a possibility. 7. We conclude that in this study we have identified models and parameters that may be used to predict spindle afferent firing from the time course of muscle length in the cat step cycle.

Figure 7. Graphical representation of the models used in this report

The analysis was performed using Matlab Simulink software. This graph can be downloaded from the Internet and a simulation run under Simulink without further programming (see Appendix text). Each model is represented as a few processing blocks, each block performing a mathematical operation on the input. These operations include computing Laplace transfer functions, implementing algebraic equations or performing simple non-linear operations such as returning an absolute value of the input signal. Presented in this form, models that were previously difficult to implement may be tested and modified with relative ease.

Figure 1. Method of computing ensemble activity during the step cycle and using mathematical models to predict either spindle firing rate from muscle length or muscle length from spindle firing rate

A, firing of a hamstring spindle primary afferent during two steps. Schematics of hindlimb at top show approximate timing of phases of the step cycles. The afferent fired most during muscle lengthening in the swing phase. Dotted vertical lines show alignment points for averaging. B, mean EMG, muscle length and afferent firing rate computed as a probability density function of impulses occurring in 10 ms bins. Nine hamstring spindle primary afferents each contributed five cycles to the average. Top panel in C, spindle primary firing rate predicted from muscle length by a mathematical model. Bottom panel in C, muscle length predicted from afferent firing rate by the inverse of the same model. The model was a power-law function of muscle velocity (see text). Note the good correspondence between predictions in C and the corresponding ‘real’ length and rate profiles in B.

Figure 2. Predictions of hamstring spindle primary afferent firing with added components mimicking α-γ linkage

The normalized mean EMG, mean length and mean rate profiles were computed from a sub-group of fast step cycles shown in Fig. 1. The same power-law model as in Fig. 1 was used. A, mean spindle primary firing rate with prediction of model superimposed. Right: linear regression of predicted rate (ordinate) plotted against ‘real’ rate (abscissa), one sample per bin. Note the good fit (high correlation coefficient and low r.m.s. error in relation to overall modulation depth). Ba, scaled EMG signal (maximum value 15). Bb, result of adding the scaled EMG of Ba to the prediction in A. Linearity of fit (as judged by r² values) was not quite as good as in A, but r.m.s. error was slightly lower. Ca, differentiated version of EMG signal. Cb, addition of Ca signal to predicted signal in A. Regression parameters show a slight deterioration of the fit compared with A. Da and b, similar data for integrated EMG. This gave a small but significant improvement over A. On balance, the data supported the existence of a small component of afferent firing linked to the EMG activity.

Figure 3

E is identical to Fig. 2A. A and B, linear transfer function models. C-F, non-linear models incorporating power-law functions of velocity. All of the models gave reasonable predictions (r² > 0.5), though A, E and F were the best. The models in E and F were essentially slightly modified versions of the linear and power-law models in A-D. Though the length-sensitive term in model F slightly detracted from the fit achieved in E, it improved performance at low muscle velocities (see Fig. 7), i.e. it was more generally valid.

Figure 8. Graphical design of hybrid model used to predict hamstring spindle primary afferent firing from muscle length

This model (rate is proportional to v^0.6 and muscle displacement) was used to give rise to Fig. 3F. This schematic design includes three boxes on the left that represent the original averaged EMG, spindle primary afferent firing fate and length signals. Details of equations used are given in the text.

Figure 6. Predictions of the models of spindle primary responses to ramp-and-hold stretches at much lower velocities than those recorded in locomotion

Dotted lines show the range of spindle primary responses under moderate static fusimotor drive, estimated from the literature (see text). Models without length-sensitive terms (e.g. c and e) did not reproduce the ramp increase in firing rate during stretch, so cannot be considered general. The responses in d and f fall in the middle of the expected range and have appropriate step and ramp components, indicating that their velocity and positional sensitivities are correctly scaled. These models also predicted the step data well (see earlier figures).

Figure 4. Comparison of the various spindle primary models in step cycles of different speeds

Predictions for data from the same nine afferents as in Figs 1–3 but with the cycles selected into three groups according to muscle velocities (see peak muscle velocity values in upper panels). The aim was to compare how well the models generalized across data when muscle velocity varied. Left column same as in Fig. 3. The r.m.s. errors in the two linear models (A and B) increased in the slow cycles whereas those of the power-law functions tended to reduce. This indicates that the power-law functions tracked velocity changes better. The best fits were seen in E and F.

Figure 5. Predictions of muscle length from spindle primary firing profiles

These were obtained by using the inverse of the models used earlier. The regression parameters in A and D indicate excellent goodness of fit. The analysis shows that in principle, the central nervous system could derive accurate estimates of muscle length from ensemble spindle primary firing rate.