Mathematical model of vertebrate gap junctions derived from electrical measurements on homotypic and heterotypic channels
- PMID: 9625876
- PMCID: PMC2231023
- DOI: 10.1111/j.1469-7793.1998.177bz.x
Mathematical model of vertebrate gap junctions derived from electrical measurements on homotypic and heterotypic channels
Abstract
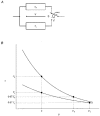
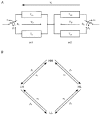
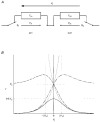
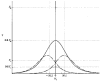
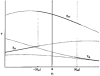
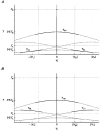
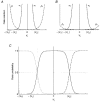
1. A mathematical model has been developed which describes the conductive and kinetic properties of homotypic and heterotypic gap junction channels of vertebrates. 2. The model consists of two submodels connected in series. Each submodel simulates a hemichannel and consists of two conductances corresponding to a high (H) and low (L) conductance state and a switch, which simulates the voltage-dependent channel gating. 3. It has been assumed that the conductances of the high state and low state vary exponentially with the voltage across the hemichannel. 4. The parameters of the exponentials can be derived from data of heterotypic or homotypic channels. As a result, the behaviour of heterotypic channels can be predicted from homotypic channel data and vice versa. 5. The two switches of a channel are governed by the voltage drop across the respective hemichannel. The switches of a channel work independently, thus giving rise to four conformational states, i.e. HH, LH, HL and LL. 6. The computations show that the dogma of a constant conductance for homotypic channels results from the limited physiological range of transjunctional voltages (Vj) and the kinetic properties of the channel, so a new fitting procedure is presented. 7. Simulation of the kinetic properties at the multichannel level revealed current time courses which are consistent with a contingent gating. 8. The calculations have also shown that the channel state LL is rare and of short duration, and hence easy to miss experimentally. 9. The design of the model has been kept flexible. It can be easily expanded to include additional features, such as channel substates or a closed state.
Figures

References
-
- Baigent S, Stark J, Warner A. Modelling the effect of gap junction nonlinearities in systems of coupled cells. Journal of Theoretical Biology. 1997;186:223–239.
-
- Banach K, Weingart R. Connexin43 gap junctions exhibit asymmetrical gating properties. Pflügers Archiv. 1996;431:775–785. - PubMed
-
- Bruzzone R, White TW, Paul DL. Connections with connexins; the molecular basis of direct intercellular signalling. European Journal of Biochemistry. 1996;238:1–27. - PubMed
-
- Bukauskas FF, Elfgang C, Willecke K, Weingart R. Heterotypic gap junction channels (connexin26-connexin32) violate the paradigm of unitary conductance. Pflügers Archiv. 1995b;429:870–872. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

