Force-velocity and power-load curves in rat skinned cardiac myocytes
- PMID: 9706028
- PMCID: PMC2231141
- DOI: 10.1111/j.1469-7793.1998.519bh.x
Force-velocity and power-load curves in rat skinned cardiac myocytes
Abstract
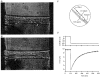
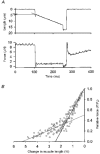
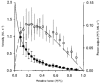
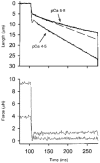
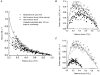
1. This study utilized a skinned myocyte preparation with low end compliance to examine force-velocity and power-load curves at 12 C in myocytes from rat hearts. 2. In maximally activated myocyte preparations, shortening velocities appeared to remain constant during load clamps in which shortening took place over a sarcomere length range of approximately 2.30-2.00 micro m. These results suggest that previously reported curvilinear length traces during load clamps of multicellular preparations were due in part to extracellular viscoelastic structures that give rise to restoring forces during myocardial shortening. 3. During submaximal Ca2+ activations, the velocity of shortening at low loads slowed and the time course of shortening became curvilinear, i.e. velocity progressively slowed as shortening continued. This result implies that cross-bridge cycling kinetics are slower at low levels of activation and that an internal load arises during shortening of submaximally activated myocytes, perhaps due to slowly detaching cross-bridges. 4. Reduced levels of activator Ca2+ also reduced maximal power output and increased the relative load at which power output was optimal. For a given absolute load, the shift has the effect of maintaining power output near the optimum level despite reductions in cross-bridge number and force generating capability at lower levels of Ca2+.
Figures

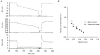

References
-
- Brady AJ. Mechanical properties of isolated cardiac myocytes. Biological Reviews. 1991;71:413–428. - PubMed
-
- Brenner B. Calcium activation and maximum unloaded shortening velocity. Investigations on glycerinated skeletal and heart muscle preparations. Basic Research in Cardiology. 1980;75:40–46. - PubMed
-
- Brenner B. The necessity of using two parameters to describe isotonic shortening velocity of muscle tissues: The effect of various interventions upon initial shortening velocity (vi) and curvature (b) Basic Research in Cardiology. 1986;81:54–69. - PubMed
-
- Brutsaert DL, Claes VA, Goethals MA. Effect of calcium on force-velocity relations of heart muscle of the cat. Circulation Research. 1973;32:385–392. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

